题目内容
若锐角α满足2sinα+2
cosα=3，则tan（α+
）= ．
| 3 |
| π |
| 3 |
考点：两角和与差的正切函数,同角三角函数基本关系的运用
专题：三角函数的求值
分析：由两角和与差的三角函数公式可得sin（α+
），再由同角三角函数的基本关系可得cos（α+
），相除可得答案．
| π |
| 3 |
| π |
| 3 |
解答：
解：∵锐角α满足2sinα+2
cosα=3，
∴
sinα+
cosα=
，
∴sin（α+
）=
，
∴cos（α+
）=±
=±
，
∴tan（α+
）=
=±
故答案为：±
| 3 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 4 |
∴sin（α+
| π |
| 3 |
| 3 |
| 4 |
∴cos（α+
| π |
| 3 |
1-sin2(α+
|
| ||
| 4 |
∴tan（α+
| π |
| 3 |
sin(α+
| ||
cos(α+
|
3
| ||
| 7 |
故答案为：±
3
| ||
| 7 |
点评：本题考查两角和与差的三角函数公式，涉及同角三角函数的基本关系，属基础题．
练习册系列答案
相关题目
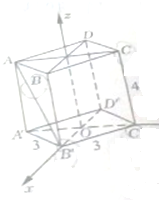已知长方体ABCD-A′B′C′D′的上，下底面都是边长为3的正方形，长方体的高为4，如图建立空间直角坐标系，求下列直线的一个方向向量．