题目内容
已知函数f(x)=x2-4x+3,集合M={(x,y)|f(x)+f(y)≤0},集合N={x,y|f(x)-f(y)≥0},则集合M∩N的面积为 .
考点:交集及其运算,二次函数的性质
专题:集合
分析:根据题意确定出M,N所表示的平面区域,两条直线x+y-4=0和x-y=0把M平均分为4份,其中两份就是M与N的交集,求出即可.
解答:
解:∵f(x)=x2-4x+3,集合M={(x,y)|f(x)+f(y)≤0},集合N={(x,y)|f(x)-f(y)≥0},
∴集合M:(x-2)2+(y-22≤2,是一个以(2,2)为圆心,
为半径的圆,面积是2π,
集合N:(x-2)2≥(y-2)2,或者(x+y-4)(x-y)≥0,
两条直线x+y-4=0和x-y=0把M平均分为4份,其中两份就是M与N的交集,
则M∩N面积=
×2π×2=
×2=π.
故答案为:π.
∴集合M:(x-2)2+(y-22≤2,是一个以(2,2)为圆心,
| 2 |
集合N:(x-2)2≥(y-2)2,或者(x+y-4)(x-y)≥0,
两条直线x+y-4=0和x-y=0把M平均分为4份,其中两份就是M与N的交集,
则M∩N面积=
| 1 |
| 4 |
| π |
| 2 |
故答案为:π.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
已知i为虚数单位,复数z=
,则复数z的实部为( )
| 1+2i |
| 1-i |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
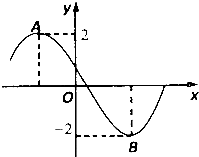 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,