题目内容
某班联欢晚会玩飞镖投掷游戏,规则如下:每人连续投掷5支飞镖,累积3支飞镖掷中目标即可获奖;否则不获奖.同时要求在以下两种情况下中止投掷:①累积3支飞镖掷中目标;②累积3支飞镖没有掷中目标.已知小明同学每支飞镖掷中目标的概率是常数p(p>0.5),且掷完3支飞镖就中止投掷的概率为
.
(1)求p的值;
(2)记小明结束游戏时,投掷的飞镖支数为X,求X的分布列和数学期望.
| 1 |
| 3 |
(1)求p的值;
(2)记小明结束游戏时,投掷的飞镖支数为X,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:(1)利用掷完3支飞镖就中止投掷的概率为
,建立方程,即可求p的值;
(2)确定X可能的取值,求出相应的概率,可得X的分布列和数学期望EX.
| 1 |
| 3 |
(2)确定X可能的取值,求出相应的概率,可得X的分布列和数学期望EX.
解答:
解:(1)由题意,p3+(1-p)3=
,
∵p>0.5,
∴p=
;
(2)X的所有可能取值为3,4,5,则
P(X=3)=
,P(X=4)=[
×(
)2×
]×
+[
×(
)2×
]×
=
,P(X=5)=
×(
)2×(
)2=
,
X的分布列
数学期望EX=3×
+4×
+5×
=
.
| 1 |
| 3 |
∵p>0.5,
∴p=
| 2 |
| 3 |
(2)X的所有可能取值为3,4,5,则
P(X=3)=
| 1 |
| 3 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
X的分布列
| X | 3 | 4 | 5 | ||||||
| P |
|
|
|
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
| 107 |
| 27 |
点评:本题考查概率的计算,考查离散型随机变量的分布列与期望,确定变量的取值,求出相应的概率是关键.

练习册系列答案
相关题目
设函数f(x)在[0,1]上的图象是连续不断的曲线,在开区间(0,1)内的导函数f′(x)恒不等于1,对任意x∈[0,1]都有0<f(x)<1,则方程f(x)=x在开区间(0,1)内实根的个数为( )
| A、4 | B、3 | C、2 | D、1 |
已知A={x∈R|x2-1>0},B={x∈Z|log2(x+3)≤2},则(∁RA)∩B)( )
| A、[-1,1] |
| B、(-3,-1) |
| C、{-1,0,1} |
| D、{0,1} |
在△ABC中,边a,b,c所对的角分别为A,B,C,若a=
,b=
,B=60°,则A=( )
| 2 |
| 3 |
| A、135° | B、45° |
| C、135°或45° | D、90° |
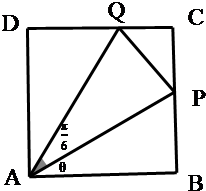 如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=
如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=