��Ŀ����
12��ij��һ���ж��꼶�����п��Ժ��������ѧ����������Ƴ�6����ѧ·��--A����ʷ��B�����ģ�C��ʫ�裬D���Ƽ���E�����磬F��̽�أ�������ÿ����·��ѡ�еĿ�������ͬ����������6����·�����ѡ��4����·������ѧ������ʷ��Ƽ�������·����ѡ�еĸ��ʣ�
������ѧ������ѧУ�Ӳμ���ѧ������ѧ���У������ȡ��100��ѧ���μӶԱ�����ѧ����ȵĵ��飬����ȵ÷ֵ�ͳ�ƽ�����±���
| ����ȵ÷� | [0��50�� | [50��60�� | [60��70�� | [70��80�� | [80��90�� | [90��100] |
| ���� | 0 | 2 | 9 | 26 | 52 | 11 |
���� ��1��ʹ���оٷ�������ʣ���2��ʹ������ֵ���汾��ƽ���֣������Ȩƽ������
��� �⣺��1����6����ѧ·�����ѡ��4���Ļ����¼�����15�֣����Ƿֱ��ǣ�ABCD������ABCE������ABCF������ABDE������ABDF������ABEF������ACDE������ACDF������ACEF������ADEF������BCDE����
��BCDF������BCEF������BDEF������CDEF���������Ƿ����Ļ�����ȣ�������ʷ�ͿƼ�����ѡ�еĸ��ʹ���6�֣������ǣ�ABCD������ABDE������ACDE������ACDF������ADEF������ABDF����
����ʷ��Ƽ�������·����ѡ�еĸ���Ϊ$\frac{6}{15}$=$\frac{2}{5}$��
��2��$\overline{x}$=$\frac{1}{100}$��55��2+65��9+75��26+85��52+95��11��=81.1
��ѧ���Ա�����ѧ����ȵ�ƽ���÷���81.1��
���� ���⿼���˹ŵ���͵ĸ��ʼ��㣬���������������ͳ��˼�룬�ǻ����⣮

��ϰ��ϵ�д�
 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
�����Ŀ
20����˫���ߵ�������ԭ�㣬������x���ϣ�������eΪ$\sqrt{5}$�����˫���ߵ����������߷���Ϊ��������
| A�� | y=��2x | B�� | y=��$\frac{1}{2}x$ | C�� | y=��4x | D�� | y=��x |
17����5�ŷֱ�д������1��2��3��4��5�Ŀ�Ƭ��ϣ��ٽ��������ų�һ�У���õ������ܱ�2��5�����ĸ����ǣ�������
| A�� | 0.2 | B�� | 0.4 | C�� | 0.6 | D�� | 0.8 |
1����������C1��y=$\frac{1}{4}$x2�Ľ���F��˫����C2��$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0����һ�������ߵľ���Ϊ$\frac{\sqrt{3}}{2}$��������C1�ϵĶ���P��˫����C2��һ������ľ����뵽ֱ��y=-1�ľ���֮�͵���СʱΪ$\sqrt{5}$����˫����C2�ķ���Ϊ��������
| A�� | $\frac{{x}^{2}}{3}$-y2=1 | B�� | x2-$\frac{{y}^{2}}{3}$=1 | C�� | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=1 | D�� | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1 |
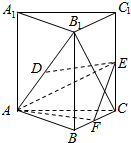 ��֪������ABC-A1B1C1�У�CC1�͵���ABC��AB=AC��D��E��F�ֱ�ΪB1A��C1C��BC���е㣮
��֪������ABC-A1B1C1�У�CC1�͵���ABC��AB=AC��D��E��F�ֱ�ΪB1A��C1C��BC���е㣮