题目内容
已知数列{an}中,a1=5,a2=2,an=2an-1+3an-2(n≥3).
(1)求数列{an}前三项之和S3的值;
(2)证明:数列{an+an-1}(n≥2)是等比数列;
(3)求数列{an}的通项公式.
(1)求数列{an}前三项之和S3的值;
(2)证明:数列{an+an-1}(n≥2)是等比数列;
(3)求数列{an}的通项公式.
考点:等比数列的性质,数列递推式
专题:等差数列与等比数列
分析:(1)根据递推式先求得a3,把前三项相加即可求得前三项之和S3的值.
(2)把已知等式两端同时加上an-1,整理可得
=3,根据等比数列的定义推断出数列{an+an-1}(n≥2)是等比数列.
(3)根据等比数列通项公式求得数列{an+an-1}的通项公式,利用拆项累和求得an,最后把n=1验证,综合可得数列{an}的通项公式.
(2)把已知等式两端同时加上an-1,整理可得
| an+an-1 |
| an-1+an-2 |
(3)根据等比数列通项公式求得数列{an+an-1}的通项公式,利用拆项累和求得an,最后把n=1验证,综合可得数列{an}的通项公式.
解答:
解:(1)∵a1=5,a2=2,an=2an-1+3an-2,
∴a3=2a2-3a1=19,
S3=a1+a2+a3=26.
(2)∵an=2an-1+3an-2,等号两端同时加上an-1,整理得an+an-1=3(an-1+an-2),
∴
=3,
∴数列{an+an-1}(n≥2)是等比数列.
(3)由(2)知,数列{an+an-1}的通项为:an+an-1=7×3n-2,n≥2,
拆项累和得:
(-1)nan=[(-1)nan-(-1)n-1an-1]+[(-1)n-1an-1-(-1)n-2an-2]+…+[(-1)2a2-(-1)a1]+(-1)a1,
=7•[(-3)n-2+(-3)n-3+…+(-3)0-5
=
-5
=-
•(-3)n-1-
,
∴an=
•(-3)n-1-
(-1)n,n≥2,
经验证知,上式对n=1也成立,
故数列的通项公式为:an=
•(-3)n-1-
(-1)n,n∈N*.
∴a3=2a2-3a1=19,
S3=a1+a2+a3=26.
(2)∵an=2an-1+3an-2,等号两端同时加上an-1,整理得an+an-1=3(an-1+an-2),
∴
| an+an-1 |
| an-1+an-2 |
∴数列{an+an-1}(n≥2)是等比数列.
(3)由(2)知,数列{an+an-1}的通项为:an+an-1=7×3n-2,n≥2,
拆项累和得:
(-1)nan=[(-1)nan-(-1)n-1an-1]+[(-1)n-1an-1-(-1)n-2an-2]+…+[(-1)2a2-(-1)a1]+(-1)a1,
=7•[(-3)n-2+(-3)n-3+…+(-3)0-5
=
| 7•[1-(-3)n-1] |
| 1+3 |
=-
| 7 |
| 4 |
| 13 |
| 4 |
∴an=
| 7 |
| 4 |
| 13 |
| 4 |
经验证知,上式对n=1也成立,
故数列的通项公式为:an=
| 7 |
| 4 |
| 13 |
| 4 |
点评:本题主要考查了等比数列的通项公式和求和公式的应用.考查了学生推理和运算的能力.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
不等式x2-3x+2>0的解集为( )
| A、(-∞,-2)∪(-1,+∞) |
| B、(-∞,1)∪(2,+∞) |
| C、(-2,-1) |
| D、(1,2) |
 如图,有一菱形纸片ABCD,∠A=60°,E是AD边上的一点(不包括A,D),先将ABCD沿对角线BD折成直二面角,再将△ABE沿BE翻折到△A′BE,下列不可能正确的是( )
如图,有一菱形纸片ABCD,∠A=60°,E是AD边上的一点(不包括A,D),先将ABCD沿对角线BD折成直二面角,再将△ABE沿BE翻折到△A′BE,下列不可能正确的是( )| A、BC与平面A′BE内某直线平行 |
| B、BC与平面A′BE内某直线垂直 |
| C、CD∥平面A′BE |
| D、CD⊥平面A′BE |
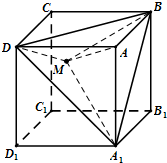 如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若f(M)=(
如图,在单位正方体ABCD-A1B1C1D1中,设M是△A1BD内任一点(不包括边界),定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-ADA1、三棱锥M-ABA1、三棱锥M-ADB的体积.若f(M)=( 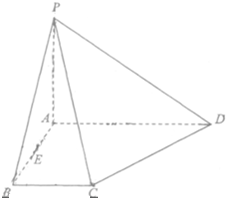 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点.