题目内容
化简:
-
.
| 3 |
| sin240° |
| 1 |
| cos240° |
考点:二倍角的余弦,二倍角的正弦
专题:三角函数的求值
分析:把所给的式子通分后利用两角和的正弦公式、二倍角公式、诱导公式化简,可得结果.
解答:
解:
-
=
=
=
=
=
=
=32sin10°.
| 3 |
| sin240° |
| 1 |
| cos240° |
(
| ||
| sin240°•cos240° |
(
| ||||
|
=
| 4sin(60°+40°)•sin(60°-40°) | ||
|
| 16sin100°sin20° |
| sin280° |
| 16sin20° |
| sin80° |
| 32sin10°cos10° |
| cos10° |
点评:本题主要考查两角和的正弦公式、二倍角公式、诱导公式化简三角函数式,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
A={x|x>0},B={x|x>1},则A∩B=( )
| A、{x|0≤x<1} |
| B、{x|0<x≤1} |
| C、{x|x<0} |
| D、{x|x>1} |
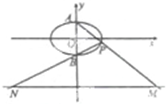 如图,已知椭圆C:
如图,已知椭圆C: