题目内容
已知 均在椭圆
均在椭圆 上,直线
上,直线 、
、 分别过椭圆的左右焦点
分别过椭圆的左右焦点 、
、 ,当
,当 时,有
时,有 .
.
(I)求椭圆 的方程;
的方程;
(II)设P是椭圆 上的任一点,
上的任一点, 为圆
为圆 的任一条直径,求
的任一条直径,求 的最大值.
的最大值.
解:(Ⅰ)因为 ,所以有
,所以有
所以 为直角三角形;
为直角三角形;
则有
所以, …………………………3分
…………………………3分
又 ,
,
在 中有
中有
即 ,解得
,解得
所求椭圆 方程为
方程为
(II)

从而将求 的最大值转化为求
的最大值转化为求 的最大值
的最大值
 是椭圆
是椭圆 上的任一点,设
上的任一点,设 ,则有
,则有 即
即
又 ,所以
,所以
而 ,所以当
,所以当 时,
时, 取最大值
取最大值
故 的最大值为
的最大值为 .
.

练习册系列答案
相关题目
 的双曲线经过点(4,
的双曲线经过点(4, ),则双曲线的方程是 ( )
),则双曲线的方程是 ( ) B.
B. C.
C. D.
D.
 的值为 .
的值为 . ,若
,若 与
与 的夹角为锐角,则x的范围是____________。
的夹角为锐角,则x的范围是____________。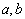 是两条不重合的直线,
是两条不重合的直线,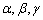 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题: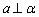 ,
,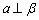 ,则
,则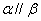 ②若
②若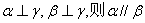
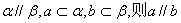 ④若
④若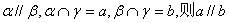
 中,a,b,c成等比数列,且
中,a,b,c成等比数列,且 ,则
,则 有最小值 .
有最小值 .  中,
中, ,
, ,当
,当 时,
时, 等于
等于 的个位数,若数列
的个位数,若数列 项和为243,则
项和为243,则 ,若函数
,若函数 ,
, 有大于零的极值点,则a的范围是 .
有大于零的极值点,则a的范围是 . ,若存在实数
,若存在实数 ,使得
,使得 成立,则实数
成立,则实数 的取值范围是( ) w
的取值范围是( ) w B.
B. C.
C. D.
D.