题目内容
5．
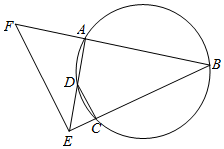如图，A，B，C，D四点共圆，BC，AD的延长线交于点E，点F在BA的延长线上，（1）若$\frac{EC}{EB}=\frac{1}{4}，\frac{ED}{EA}=\frac{1}{2}，求\frac{DC}{AB}$的值；
（2）若EF2=FA•FB，证明：EF∥CD．
分析 （1）推导出△EDC∽△EBA，由此能求出$\frac{DC}{AB}$的值．
（2）推导出△FAE∽△FEB，从而∠FEA=∠EBF，再由四点共圆，能证明EF∥CD．
解答 解：（1）∵A、B、C、D四点共圆，
∴∠ECD=∠EAB，∠EDC=∠B，
∴△EDC∽△EBA，∴$\frac{ED}{EB}=\frac{EC}{EA}=\frac{DC}{AB}$，
$\frac{ED}{EB}•\frac{EC}{EA}$=$（\frac{DC}{AB}）^{2}$=$\frac{1}{8}$，
∴$\frac{DC}{AB}$=$\frac{\sqrt{2}}{4}$．
证明：（2）∵EF2=FA•FB，∴$\frac{EF}{FA}=\frac{FB}{EF}$，
∵∠EFA=∠BFE，
∴△FAE∽△FEB，
∴∠FEA=∠EBF，
∵A、B、C、D四点共圆，∠EDC=∠EBF，
∴∠FEA=∠EDC，∴EF∥CD．
点评 本题考查两线段比值的求法，考查两直线平行的证明，是中档题，解题时要认真审题，注意圆的简单性质、三角形相似的性质的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．若P点是以F1（-3，0）、F2（3，0）为焦点，实轴长为4的双曲线与圆x2+y2=9的一个交点，则|PF1|+|PF2|=（ ）
| A． | $\sqrt{13}$ | B． | 6 | C． | 2$\sqrt{14}$ | D． | 2$\sqrt{5}$ |
20．若椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1与$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的离心率分别为e1，e2，且e1+e2=$\sqrt{3}$，则e1e2=（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |