题目内容
12．如图，一渡船自岸边A处出发，与岸边成70°方向以30kmh的速度航行，由于河水流速的影响，它实际航行的方向与河岸成120°，试求水流速度（水流方向与河岸平行，精确到0.1km/h
分析 船的航行速度和水流速度都可用向量表示，根据向量加法的平行四边形法则作平行四边形OABC，其中OA=30，∠AOB=50°，∠BOC=60°，这样由正弦定理即可求出AB的长度，即得出水流的速度．
解答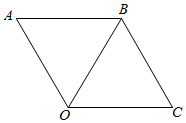 
解：如图，作平行四边形OABC，使OA=30，∠AOB=50°，∠BOC=60°则
向量$\overrightarrow{OC}$表示水流的速度；
在△AOB中，由正弦定理得：$\frac{AB}{sin50°}=\frac{30}{sin60°}$；
∴$AB=\frac{sin50°}{sin60°}•30$≈26.5；
∴水流速度为26.5km/h．
点评 考查向量加法的平行四边形法则，速度的合成，以及正弦定理．
练习册系列答案
相关题目
3．已知函数f（x）=sinωx-cosωx，ω＞0是常数，x∈R，且图象上相邻两个最高点的距离为π，则下列说法正确的是（ ）
| A． | ω=1 | B． | 曲线y=f（x）关于点（π，0）对称 | ||
| C． | 曲线y=f（x）与直线$x=\frac{π}{2}$对称 | D． | 函数f（x）在区间$（0，\frac{π}{3}）$单调递增 |
17．已知等比数列{an}中，a2=2，又a2，a3+1，a4成等差数列，数列{bn}的前n项和为Sn，且$\frac{1}{{S}_{n}}$=$\frac{1}{n}$-$\frac{1}{n+1}$，则a8+b8=（ ）
| A． | 311 | B． | 272 | C． | 144 | D． | 80 |
4．双曲线的离心率e=$\sqrt{2}$，经过M（-5，3）的方程是（ ）
| A． | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1 | B． | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{16}$=1 | C． | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{9}$=1 | D． | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{9}$=1 |
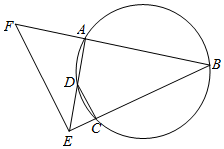如图，A，B，C，D四点共圆，BC，AD的延长线交于点E，点F在BA的延长线上，