题目内容
13.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右顶点为A,经过原点的直线l交椭圆C于P、Q两点,若|PQ|=a,AP⊥PQ,则椭圆C的离心率为$\frac{2\sqrt{5}}{5}$.分析 设点P在第一象限,由对称性可得|OP|=$\frac{|PQ|}{2}$=$\frac{a}{2}$,推导出∠POA=60°,P($\frac{a}{4},\frac{\sqrt{3}a}{4}$),由此能求出椭圆的离心率.
解答 解:不妨设点P在第一象限,由对称性可得|OP|=$\frac{|PQ|}{2}$=$\frac{a}{2}$,
∵AP⊥PQ,在Rt△POA中,cos∠POA=$\frac{|OP|}{|OA|}$=$\frac{1}{2}$,
∴∠POA=60°,∴P($\frac{a}{4},\frac{\sqrt{3}a}{4}$),
代入椭圆方程得:$\frac{{a}^{2}}{16{a}^{2}}+\frac{3{a}^{2}}{16{b}^{2}}$=1,
∴a2=5b2=5(a2-c2),整理得2a=$\sqrt{5}$c,
∴离心率e=$\frac{c}{a}$=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查椭圆的离心率的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
4.双曲线的离心率e=$\sqrt{2}$,经过M(-5,3)的方程是( )
| A. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{9}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{16}$=1 | C. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{9}$=1 | D. | $\frac{{y}^{2}}{25}$-$\frac{{x}^{2}}{9}$=1 |
1.圆锥曲线$\frac{x^2}{m}$+y2=1的离心率为$\sqrt{7}$,则m=( )
| A. | $\frac{1}{6}$ | B. | 6 | C. | -$\frac{1}{6}$ | D. | -6 |
8.已知椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0).双曲线C2:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的渐近线方程为x$±\sqrt{3}$y=0,则C1与C2的离心率之积为( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{6}}}{5}$ | D. | $\frac{{2\sqrt{2}}}{3}$ |
3.已知z(2+i)=1+ai,a∈R,i为虚数单位,若z为纯虚数,则a=( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
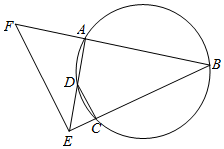 如图,A,B,C,D四点共圆,BC,AD的延长线交于点E,点F在BA的延长线上,
如图,A,B,C,D四点共圆,BC,AD的延长线交于点E,点F在BA的延长线上,