题目内容
17.在平面直角坐标系中,求方程$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1对应的图形经过伸缩变换$\left\{\begin{array}{l}x′=\frac{1}{2}x\\ y′=\frac{1}{3}y\end{array}$后得到得图形得方程为x2-y2=1.分析 利用伸缩变换$\left\{\begin{array}{l}x′=\frac{1}{2}x\\ y′=\frac{1}{3}y\end{array}$,可得x=3x′,y=2y′,代入$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1,即可得出结论.
解答 解:∵$\left\{\begin{array}{l}x′=\frac{1}{2}x\\ y′=\frac{1}{3}y\end{array}$,
∴x=2x′,y=3y′,
∵$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1,
∴x′2-y′2=1,
∴x2-y2=1,
故答案为x2-y2=1.
点评 本题考查伸缩变换,考查双曲线的方程,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知Sn是等差数列an的前n项和,且S3=2a1,则下列结论错误的是( )
| A. | a4=0 | B. | S4=S3 | C. | S7=0 | D. | an是递减数列 |
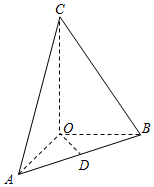 在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.
在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.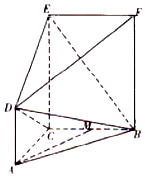 在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.
在如图所示的五面体ABCDEF中,矩形BCEF所在的平面ABC垂直,AD∥CE,CE=2AD=2,M是BC的中点,在△ABC中,∠BAC=60°,AB=2AC=2.