题目内容
12.某射手射击1次,命中目标的概率为0.9,他连续射击4次,且各次射击是否命中目标相互之间没有影响,有下列结论:①他第3次击中目标的概率是0.9;
②他恰好击中目标3次的概率为0.93×0.1;
③他至少击中目标1次的概率是1-(0.1)4;
④他最后一次才击中目标的概率是$C_4^1×0.9×{0.1^3}$
其中正确结论的序号是①③ (写出所有正确结论的序号)
分析 在①中,由概率的等可能性得他第3次击中目标的概率是0.9;在②中,利用n次独立重复试验中事件A恰好发生k次的概率计算公式能求出他恰好击中目标3次的概率;在③中,利用n次独立重复试验中事件A恰好发生k次的概率计算公式和对立事件概率计算公式能求出他至少击中目标1次的概率;在④中,利用相互独立事件概率乘法公式能求出他最后一次才击中目标的概率.
解答 解:由某射手射击1次,命中目标的概率为0.9,他连续射击4次,且各次射击是否命中目标相互之间没有影响,知:
在①中,由概率的等可能性得他第3次击中目标的概率是0.9,故①正确;
在②中,他恰好击中目标3次的概率为p=${C}_{4}^{3}•0.{9}^{3}•0.1$,故②错误;
在③中,他至少击中目标1次的概率是p=1-${C}_{4}^{0}0.{9}^{0}•0.{1}^{3}$=1-(0.1)4,故③正确;
在④中,他最后一次才击中目标的概率是p=0.13•0.9,故④错误.
故答案为:①③.
点评 本题考查概率的等可能性、n次独立重复试验中事件A恰好发生k次的概率计算公式、对立事件概率计算公式、相互独立事件概率乘法公式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.设复数z与$\frac{1+3i}{1-i}$在复平面内对应的点关于实轴对称,则z等于( )
| A. | -1+2i | B. | 1+2i | C. | 1-2i | D. | -1-2i |
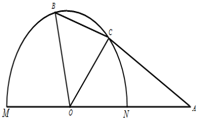 如图,半径为1的半圆O上有一动点B,MN为直径,A为半径ON延长线上的一点,且OA=2,∠AOB的角平分线交半圆于点C.
如图,半径为1的半圆O上有一动点B,MN为直径,A为半径ON延长线上的一点,且OA=2,∠AOB的角平分线交半圆于点C.