题目内容
15．已知Sn是等差数列an的前n项和，且S3=2a1，则下列结论错误的是（ ）| A． | a4=0 | B． | S4=S3 | C． | S7=0 | D． | an是递减数列 |
分析 设等差数列{an}的公差为d．由S3=2a1，可得：a1+a2+a3═3a1+3d=2a1，可得a1=-3d．利用通项公式与求和公式即可判断出A，B，C的正误．由于无法判断d的正负，因此无法判断等差数列{an}的单调性，即可判断出D的正误．
解答 解：设等差数列{an}的公差为d．
由S3=2a1，可得：a1+a2+a3═3a1+3d=2a1，可得a1=-3d．
则a4=-3d+3d=0，S4=S3，S7=$\frac{7（{a}_{1}+{a}_{7}）}{2}$=7a4=0，因此A，B，C正确．
由于无法判断d的正负，因此无法判断等差数列{an}的单调性，因此D错误．
故选：D．
点评 本题考查了等差数列的通项公式与求和公式及其性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
口算题天天练系列答案
相关题目
6．
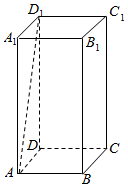如图，长方体ABCD-A1B1C1D1中，AA1=2AB=2BC=2，则异面直线A1B与AD1所成角的余弦值为（ ）
如图，长方体ABCD-A1B1C1D1中，AA1=2AB=2BC=2，则异面直线A1B与AD1所成角的余弦值为（ ）| A． | $\frac{\sqrt{10}}{10}$ | B． | $\frac{3}{5}$ | C． | $\frac{\sqrt{10}}{5}$ | D． | $\frac{4}{5}$ |