题目内容
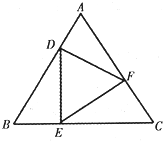如图，等边△DEF的顶点D，E，F分别在等边△ABC的边AB，BC，CA上，若在△ABC内随机取一点，则该点取自△DEF内部的概率的最小值为考点：几何概型
专题：概率与统计
分析：等边△DEF的顶点D，E，F分别在等边△ABC的边AB，BC，CA上，当D，E，F分别中点时，△DEF面积最小，为△ABC面积的
，进而得到答案．
| 1 |
| 4 |
解答：
解：∵等边△DEF的顶点D，E，F分别在等边△ABC的边AB，BC，CA上，
∴当D，E，F分别中点时，△DEF面积最小，
此时：
=
，
∴该点取自△DEF内部的概率的最小值为
，
故答案为：
∴当D，E，F分别中点时，△DEF面积最小，
此时：
| S△DEF |
| S△ABC |
| 1 |
| 4 |
∴该点取自△DEF内部的概率的最小值为
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题考查的知识点是几何概型中的面积问题，难度不大，属于基础题．
练习册系列答案
相关题目
函数y=
的定义域是（ ）
| (x+1)0 | ||
|
| A、{x|0≤x≤1} |
| B、{x|x＜-1或x＞-1} |
| C、{x|x＞0} |
| D、{x|x≠-1，x≠0} |