题目内容
函数y=
的定义域是( )
| (x+1)0 | ||
|
| A、{x|0≤x≤1} |
| B、{x|x<-1或x>-1} |
| C、{x|x>0} |
| D、{x|x≠-1,x≠0} |
考点:函数的定义域及其求法
专题:函数的性质及应用
分析:根据被开方数大于等于0,分母不为0,0的0次幂无意义,解不等式即可.
解答:
解:要使函数有意义,则
,
解得x>0,则函数的定义域是{x|x>0}.
故选:C.
|
解得x>0,则函数的定义域是{x|x>0}.
故选:C.
点评:本题考查函数的定义域及求法,以及简单绝对值不等式的解法,是基础题.

练习册系列答案
相关题目
若D、E为△ABC中AB、AC的中点,现有质地均匀的粒子散落在△ABC内,则粒子在△ADE内的概率等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一个赛跑机器人有如下特性:(1)步长可以人为地设置成0.1米,0.2米,0.3米,…,1.8米,1.9米;(2)发令后,机器人第一步立刻迈出设置的步长,且每一步的行走过程都在瞬时完成;(3)当设置的步长为a米时,机器人每相邻两个迈步动作恰需间隔a秒.则这个机器人跑50米(允许超出50米)所需的最少时间是( )
| A、48.6秒 | B、47.6秒 |
| C、48秒 | D、47秒 |
下列程序框图中,若输入n=10,得到的结果是( )


| A、55 | B、285 |
| C、385 | D、506 |
如果命题“p且q”是假命题,“非p”是真命题,那么( )
| A、命题p 一定是真命题 |
| B、命题q 一定是真命题 |
| C、命题q 可以是真命题也可以是假命题 |
| D、命题q 一定是假命题 |
设f(x+2)=2x+1,则f(2)等于( )
| A、1 | B、2 | C、3 | D、4 |
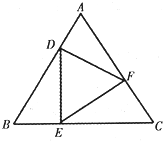 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,若在△ABC内随机取一点,则该点取自△DEF内部的概率的最小值为
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,若在△ABC内随机取一点,则该点取自△DEF内部的概率的最小值为