题目内容
一个直径AB等于2的半圆,过A作这个圆所在平面的垂线,在垂线上取一点S,使AS=AB,C为半圆上的一个动点,M、N分别为A在SB、SC上的射影.当三棱锥S-AMN的体积最大时,SC与平面ABC所成角的正弦值是 .
考点:棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:空间位置关系与距离
分析:易知BC⊥平面SAC,进而结合线面垂直的判定和性质,可得SM⊥平面AMN,当AN=MN=1时平面AMN取最大值,进而得到答案.
解答:
解:如下图所示:SA⊥平面ABC,BC?平面ABC,
∴SA⊥BC,又由BC⊥AC,SA∩AC=A,SA,AC?平面SAC,
∴BC⊥平面SAC,

又由AN?平面SAC,
∴BC⊥AN,
又由AN⊥SC,SC∩BC=C,SC,BC?平面SBC,
∴AN⊥平面SBC,
又由SB?平面SBC,
∴AN⊥SB,
又由AM⊥SB,AN∩AM=A,AN,AM?平面AMN,
∴SB⊥平面AMN,
即SM为三棱锥S-AMN中平面AMN上的高,
∵SA=AB=2,
∴AM=SM=
,
而AN⊥MN,
故△AMN是斜边为
的直角三角形,
故当AN=MN=1时,△AMN的面积S取最大值,
此时三棱锥S-AMN的体积取最大值,
此时SC与平面ABC所成角∠SCA满足,
cos∠SCA=
,
则sin∠SCA=
,
故答案为:
∴SA⊥BC,又由BC⊥AC,SA∩AC=A,SA,AC?平面SAC,
∴BC⊥平面SAC,

又由AN?平面SAC,
∴BC⊥AN,
又由AN⊥SC,SC∩BC=C,SC,BC?平面SBC,
∴AN⊥平面SBC,
又由SB?平面SBC,
∴AN⊥SB,
又由AM⊥SB,AN∩AM=A,AN,AM?平面AMN,
∴SB⊥平面AMN,
即SM为三棱锥S-AMN中平面AMN上的高,
∵SA=AB=2,
∴AM=SM=
| 2 |
而AN⊥MN,
故△AMN是斜边为
| 2 |
故当AN=MN=1时,△AMN的面积S取最大值,
此时三棱锥S-AMN的体积取最大值,
此时SC与平面ABC所成角∠SCA满足,
cos∠SCA=
| 1 |
| 2 |
则sin∠SCA=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查的知识点是棱锥的体积,直线与平面所成的角,其中分析出棱锥体积取最大值时,AN=1是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列程序框图中,若输入n=10,得到的结果是( )


| A、55 | B、285 |
| C、385 | D、506 |
 如图是某班甲、乙两个小组各7名同学在一次考试中的成绩的茎叶图,则甲、乙两个小组成绩的中位数之和为
如图是某班甲、乙两个小组各7名同学在一次考试中的成绩的茎叶图,则甲、乙两个小组成绩的中位数之和为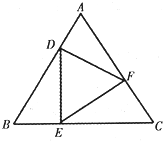 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,若在△ABC内随机取一点,则该点取自△DEF内部的概率的最小值为
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,若在△ABC内随机取一点,则该点取自△DEF内部的概率的最小值为