题目内容
已知f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=(c)=0,现给出如下结论:
①f(0)=f(3);
②f(0)f(1)<0;
③f(1)f(3)<0;
④a2+b2+c2=18.
其中正确结论个数为( )
①f(0)=f(3);
②f(0)f(1)<0;
③f(1)f(3)<0;
④a2+b2+c2=18.
其中正确结论个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数的性质
专题:函数的性质及应用
分析:根据f(x)=x3-6x2+9x-abc,a<b<c,且f(a)=f(b)=f(c)=0,确定函数的极值点及a、b、c的大小关系,由此可得结论
解答:
解:求导函数可得f′(x)=3x2-12x+9=3(x-1)(x-3)
∴当1<x<3时,f'(x)<0;当x<1,或x>3时,f'(x)>0
所以f(x)的单调递增区间为(-∞,1)和(3,+∞)单调递减区间为(1,3)
所以f(x)极大值=f(1)=1-6+9-abc=4-abc,
f(x)极小值=f(3)=27-54+27-abc=-abc
要使f(x)=0有三个解a、b、c,那么结合函数f(x)草图可知:
a<1<b<3<c
及函数有个零点x=b在1~3之间,
所以f(1)=4-abc>0,且f(3)=-abc<0
所以0<abc<4
∵f(0)=-abc,
∴f(0)=f(3)
∴f(0)<0
∴f(0)f(1)<0,f(1)f(3)<0,
∵f(a)=f(b)=(c)=0,
∴x3-6x2+9x-abc
=(x-a)(x-b)(x-c)
=x3-(a+b+c)x2+(ab+ac+bc)x-abc,
∴a+b+c=6①,ab+ac+bc=9②,
把②代入①2得:a2+b2+c2=18;
故答案为:①②③④
∴当1<x<3时,f'(x)<0;当x<1,或x>3时,f'(x)>0
所以f(x)的单调递增区间为(-∞,1)和(3,+∞)单调递减区间为(1,3)
所以f(x)极大值=f(1)=1-6+9-abc=4-abc,
f(x)极小值=f(3)=27-54+27-abc=-abc
要使f(x)=0有三个解a、b、c,那么结合函数f(x)草图可知:
a<1<b<3<c
及函数有个零点x=b在1~3之间,
所以f(1)=4-abc>0,且f(3)=-abc<0
所以0<abc<4
∵f(0)=-abc,
∴f(0)=f(3)
∴f(0)<0
∴f(0)f(1)<0,f(1)f(3)<0,
∵f(a)=f(b)=(c)=0,
∴x3-6x2+9x-abc
=(x-a)(x-b)(x-c)
=x3-(a+b+c)x2+(ab+ac+bc)x-abc,
∴a+b+c=6①,ab+ac+bc=9②,
把②代入①2得:a2+b2+c2=18;
故答案为:①②③④
点评:本题考查函数的零点、极值点,解不等式,综合性强,利用数形结合可以使本题直观.

练习册系列答案
相关题目
下列程序框图中,若输入n=10,得到的结果是( )


| A、55 | B、285 |
| C、385 | D、506 |
如果命题“p且q”是假命题,“非p”是真命题,那么( )
| A、命题p 一定是真命题 |
| B、命题q 一定是真命题 |
| C、命题q 可以是真命题也可以是假命题 |
| D、命题q 一定是假命题 |
设全集U=R,函数y=lg(2-x)的定义域为A,则∁∪A等于( )
| A、[2,+∞) |
| B、(-∞,2) |
| C、(0,2) |
| D、[0,2) |
设命题p:ax2+2ax+1>0的解集是实数集R;q:0<a<1,则p是q的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设“p是q的充分条件”;“q是r的充要条件”;“r是s的必要条件”,那么s是p的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设f(x+2)=2x+1,则f(2)等于( )
| A、1 | B、2 | C、3 | D、4 |
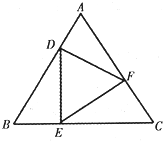 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,若在△ABC内随机取一点,则该点取自△DEF内部的概率的最小值为
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,若在△ABC内随机取一点,则该点取自△DEF内部的概率的最小值为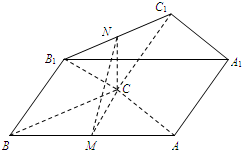 如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.