题目内容
设Sn为数列{an}的前n项和,Sn=
,则S2014= .
|
考点:数列的求和
专题:等差数列与等比数列
分析:由已知得Sn=(-1)nan-
,从而得到an=-
,n为正奇数,an=
,(n为正偶数),进而得到a1+a2=0,a3+a4=0,a5+a6=0,…a2013+a2014=0,由此能求出S2014=a1+a2+a3+a4+…+a2014=0.
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n |
解答:
解:由已知得Sn=(-1)nan-
,
当n=1时,a1=-a1-
,解得a1=-
;
当n≥2时,an=Sn-Sn-1=(-1)nan-
-(-1)n-1an-1+
,
∴an=(-1)nan+(-1)nan-1+
,
当n为偶数,an-1=-
,n≥2,
∴an=-
,n为正奇数;
当n为奇数时,an-1=-2an+
=(-2)•(-
)+
=
,
∴an=
,(n为正偶数),
∴-a1=-(-
)=
,a2=
,
则a1+a2=0
同理,a3+a4=0,
a5+a6=0,
…
a2013+a2014=0,
∴S2014=a1+a2+a3+a4+…+a2014=0.
故答案为:0.
| 1 |
| 2n |
当n=1时,a1=-a1-
| 1 |
| 2 |
| 1 |
| 4 |
当n≥2时,an=Sn-Sn-1=(-1)nan-
| 1 |
| 2n |
| 1 |
| 2n-1 |
∴an=(-1)nan+(-1)nan-1+
| 1 |
| 2n |
当n为偶数,an-1=-
| 1 |
| 2n |
∴an=-
| 1 |
| 2n+1 |
当n为奇数时,an-1=-2an+
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n |
| 1 |
| 2n-1 |
∴an=
| 1 |
| 2n |
∴-a1=-(-
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 22 |
则a1+a2=0
同理,a3+a4=0,
a5+a6=0,
…
a2013+a2014=0,
∴S2014=a1+a2+a3+a4+…+a2014=0.
故答案为:0.
点评:本题考查数列的前2014项的和的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
相关题目
如果命题“p且q”是假命题,“非p”是真命题,那么( )
| A、命题p 一定是真命题 |
| B、命题q 一定是真命题 |
| C、命题q 可以是真命题也可以是假命题 |
| D、命题q 一定是假命题 |
 如图是某班甲、乙两个小组各7名同学在一次考试中的成绩的茎叶图,则甲、乙两个小组成绩的中位数之和为
如图是某班甲、乙两个小组各7名同学在一次考试中的成绩的茎叶图,则甲、乙两个小组成绩的中位数之和为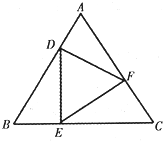 如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,若在△ABC内随机取一点,则该点取自△DEF内部的概率的最小值为
如图,等边△DEF的顶点D,E,F分别在等边△ABC的边AB,BC,CA上,若在△ABC内随机取一点,则该点取自△DEF内部的概率的最小值为