题目内容
9．圆锥底面半径为2，母线与底面成60°角，三棱锥S-ABC的顶点S是圆锥的顶点，侧棱SA、SB、SC都是圆锥的母线，则三棱锥S-ABC体积的最大值为6．分析 要使三棱锥S-ABC体积最大，只需△ABC的面积最大，此时为圆的内接等边三角形，边长为2$\sqrt{3}$，求出其面积，即可求出三棱锥S-ABC体积的最大值．
解答 解：∵圆锥底面半径为2，母线与底面成60°角，
∴圆锥的高为2$\sqrt{3}$，
要使三棱锥S-ABC体积最大，只需△ABC的面积最大，此时为圆的内接等边三角形，边长为2$\sqrt{3}$，面积为$\frac{\sqrt{3}}{4}×12$=3$\sqrt{3}$，
∴三棱锥S-ABC体积的最大值为$\frac{1}{3}×3\sqrt{3}×2\sqrt{3}$=6．
故答案为：6．
点评 本题考查求三棱锥S-ABC体积的最大值，考查学生的计算能力，正确转化是关键．
练习册系列答案
相关题目
19．在△ABC中，若（sinA+sinB）：（sinA+sinC）：（sinB+sinC）=4：5：6，且该三角形面积为15$\sqrt{3}$，则△ABC最大边长为（ ）
| A． | 7 | B． | 14 | C． | 6 | D． | 12 |
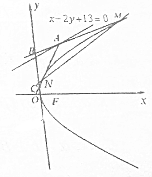过直线x-2y+13=0上一动点A（A不在y轴上）作抛物线y2=8x的两条切线，M，N为切点，直线AM，AN分别与y轴交于点B，C．
已知圆C1的方程为x2+y2=2，抛物线C2的方程为y2=4x，过直线x=-2上的动点T（-2，t）作圆C1的两条切线，设切点分别为A和B．