题目内容
20.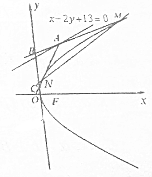 过直线x-2y+13=0上一动点A(A不在y轴上)作抛物线y2=8x的两条切线,M,N为切点,直线AM,AN分别与y轴交于点B,C.
过直线x-2y+13=0上一动点A(A不在y轴上)作抛物线y2=8x的两条切线,M,N为切点,直线AM,AN分别与y轴交于点B,C.(1)证明直线MN恒过一定点;
(2)证明△ABC的外接圆恒过一定点,并求该圆半径的最小值.
分析 (1)利用切线方程都过A,求出直线MN的方程,结合A在直线x-2y+13=0上,即可证明直线MN恒过一定点;
(2)确定A,B,C,F四点共圆,AF为直径,即可求解.
解答 (1)证明:设M(x1,y1),N(x2,y2),A(x0,y0),
切线AM的方程为y1y=4(x+x1),AN的方程为y2y=4(x+x2),
∵两条切线都过A,
∴M,N在y0y=4(x+x0)上,
∵x0-2y0+13=0,
∴联立可得4(x-13)=y0(y-8),
∴直线MN恒过一定点(13,8);
(2)由题意,抛物线的焦点坐标为F(2,0),切线AM的方程为y1y=4(x+x1),B(0,$\frac{4{x}_{1}}{{y}_{1}}$),
∴kBF=-$\frac{2{x}_{1}}{{y}_{1}}$,
∵kBA=$\frac{4}{{y}_{1}}$,
∴kBFkBA=-$\frac{8{x}_{1}}{{{y}_{1}}^{2}}$=-1,
∴BF⊥BA.
同理可得CF⊥CA,
∴A,B,C,F四点共圆,AF为直径,
∴△ABC的外接圆恒过一定点F(2,0),
由AF的最小值=点F到直线x-2y+13=0的距离d=3$\sqrt{5}$,可得圆半径的最小值为$\frac{3}{2}$$\sqrt{5}$.
点评 本题考查直线过定点,考查△ABC的外接圆恒过一定点,考查学生分析解决问题的能力,确定抛物线的切线方程是关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
11.已知直线l的一般方程式为x+y+1=0,则l的一个方向向量为( )
| A. | (1,1) | B. | (1,-1) | C. | (1,2) | D. | (1,-2) |
10.关于x的方程m=$\frac{4x}{{x}^{2}+4}$的解个数不可能是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |