题目内容
19．求值：（1）sin[2arcsin（-$\frac{3}{5}$）]
（2）tan（$\frac{1}{2}$arccos$\frac{1}{3}$）
分析 （1）利用反三角函数的定义，二倍角的正弦公式，求得要求式子的值．
（2）利用反三角函数的定义，半角的正切公式，求得要求式子的值．
解答 解：（1）sin[2arcsin（-$\frac{3}{5}$）]=2sin[arcsin（-$\frac{3}{5}$）]cos[arcsin（-$\frac{3}{5}$）]
=2•（-$\frac{3}{5}$）•$\frac{4}{5}$=-$\frac{24}{25}$．
（2）∵tan（$\frac{1}{2}$arccos$\frac{1}{3}$）=$\frac{1-cos（arccos\frac{1}{3}）}{sin（arccos\frac{1}{3}）}$=$\frac{1-\frac{1}{3}}{\frac{2\sqrt{2}}{3}}$=$\frac{\sqrt{2}}{2}$．
点评 本题主要考查反三角函数的定义，二倍角的正弦公式、半角的正切公式的应用，属于基础题．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
10．关于x的方程m=$\frac{4x}{{x}^{2}+4}$的解个数不可能是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
14．直线7x+3y-21=0上到两坐标轴距离相等的点的个数为（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 0 |
4．已知角α的始边与x轴的正半轴重合，顶点在坐标原点，角α终边上的一点P到原点的距离为$\sqrt{2}$，若α=$\frac{π}{4}$，则点P的坐标为（ ）
| A． | （1，$\sqrt{2}$） | B． | （$\sqrt{2}$，1） | C． | （$\sqrt{2}$，$\sqrt{2}$） | D． | （1，1） |
11．不等式$\frac{1+|x|}{|x|-3}$≥3的解集为（ ）
| A． | （-5，-3）∪（3，5） | B． | [-5，-3）∪（3，5] | C． | （-5，-3） | D． | （3，5） |
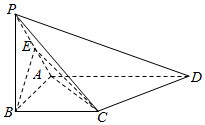在四棱锥P-ABCD中，△ABC，△ACD都为等腰直角三角形，∠ABC=∠ACD=90°，E为PA的中点．