题目内容

在△ABC中，A=60°，a=
13
，则
a+b+c
sinA+sinB+sinC
等于（　　）
A、
8
3
3
B、
2
39
3
C、
26
3
3
D、2
3
考点：正弦定理的应用
专题：计算题
分析：由正弦定理及已知可得a=
2
39
3
sinA，b=
2
39
3
sinB，c=
2
39
3
sinC，则
a+b+c
sinA+sinB+sinC
=
2
39
3
(sinA+sinB+sinC)
sinA+sinB+sinC
=
2
39
3
．
解答： 解：由正弦定理
a
sinA
=
b
sinB
=
c
sinC

a
sinA
=
13
3
2
=
2
39
3

∴a=
2
39
3
sinA，b=
2
39
3
sinB，c=
2
39
3
sinC
则
a+b+c
sinA+sinB+sinC

=
2
39
3
(sinA+sinB+sinC)
sinA+sinB+sinC

=
2
39
3

故选：B．
点评：本题主要考查了正弦定理的应用，属于基础题．
练习册系列答案
相关题目
不等式|x-2|+|x+1|≤5为
 
．
数列{an}的首项为a1=2且an+1=
1
2
（a1+a2+…+an）（n∈N*），记Sn为数列{an}的前n项和，则数列{Sn}的前n项和Tn=
 
．
与圆x2+y2+4x+2=0相切，且在x轴、y轴上的截距之比为1：1的直线共有
 
条．
一个几何体的三视图如图，其俯视图是一个等边三角形，则这个几何体的体积为（　　）
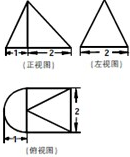
A、
(4+π)
3
3
B、
(8+π)
3
6
C、
(8+π)
3
3
D、（4+π）
3
一个容量为20的样本数据分组后，分组与频数分别如下：（10，20]，2；（20，30]，3；（30，40]，4；（40，50]，5；（50，60]，4；（60，70]，2；则样本在（15，50]上的频率是
 
．
“m=1”是“直线mx+（2m-1）y+1=0和直线3x+my-3=0垂直”的（　　）
A、充分而不必要条件
B、必要而不充分条件
C、充分必要条件
D、既不充分也不必要条件
解关于x的不等式
k(1-x)
x-2
+1＜0（k≥1）．
如图，在半径为1的圆内有四段以1为半径的相等弧，现向园内投掷一颗豆子（假设豆子不落在线上），则恰好落在阴影部分的概率为（　　）
A、
π
2
B、
4-π
π
C、
π
4
D、
8-π
π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网