题目内容

已知sinθ=2cosθ，其中θ∈（0，
π
2
）．
（1）求sinθ和cosθ的值；
（2）若5cos（θ-φ）=3
5
cosφ，0＜φ＜
π
2
，求cosφ的值．
考点：同角三角函数基本关系的运用,两角和与差的余弦函数
专题：计算题,三角函数的求值
分析：（1）sinθ=2cosθ，与sin2θ+cos2θ=1联立求解；
（2）将5cos（θ-φ）=3
5
cosφ，利用两角和差三角函数公式求解，即可得出结论．
解答： 解：（1）∵sinθ=2cosθ，θ∈（0，
π
2
），sin2θ+cos2θ=1，
∴sinθ=
2
5
5
，cosθ=
5
5
；
（2）5cos（θ-φ）=3
5
cosφ，
∴5cosθcosφ+5sinθsinφ=3
5
cosφ，
∴
5
cosφ+2
5
sinφ=3
5
cosφ，
∴tanφ=1，
∵0＜φ＜
π
2
，
∴cosφ=
2
2
．
点评：本题考查同角三角函数基本关系式，两角和差三角函数公式的应用．考查公式应用能力，运算求解能力．
练习册系列答案
相关题目
若f（x）是定义在[-2，2]上的奇函数，且在[0，2]上单调递减，若f（m）+f（m-1）＜0，则实数m的取值范围是（　　）
A、[-1，
1
2
）
B、（
1
2
，2]
C、（
1
2
，+∞）
D、（-∞，
1
2
）
“实数m=-
1
2
”是“直线l1：x+2my-1=0和直线l2：（3m+1）x-my-1=0”相互平行的（　　）
A、充要条件
B、必要不充分条件
C、充分不必要条件
D、既不充分也不必要条件
数列{an}中，a1=1，它的前n项和为Sn，且
2Sn
(n+1)2
=
2Sn-1
n2
+
1
n(n+1)
（n≥2，n∈N*）．
（1）证明：
4Sn
(n+1)2
+
2
n(n+1)
=1，并求数列{an}的通项公式；
（2）当n＞1，n∈N*时，证明：（1+
1
2a2-1
）（1+
1
2a3-1
）…（1+
1
2an-1
）＞
2an+1
2
．
要得到函数y=2cos（2x-
π
6
）的图象，只要将函数y=2cos2x的图象（　　）
A、向左平行移动
π
6
个单位长度
B、向右平行移动
π
6
个单位长度
C、向左平行移动
π
12
个单位长度
D、向右平行移动
π
12
个单位长度
△ABC的内角A，B，C的对边分别为a，b，c，且asinA+csinC+
2
asinC=bsinB，则∠B=
 
．
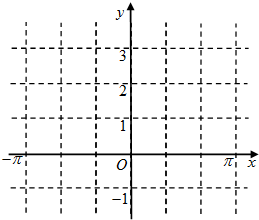已知函数f（x）=2sin（2ωx+
π
6
）+1（其中0＜ω＜1），若点（-
π
6
，1）是函数f（x）图象的一个对称中心，
（1）试求ω的值；
（2）先列表，再作出函数f（x）在区间x∈[-π，π]上的图象．
在等差数列{an}中，a3=3，a8=15，则S10=（　　）
A、30B、60C、90D、120
在自然界中，存在着大量的周期函数，比如声波，若两个声波随时间的变化规律分别为：y1=3sin（100πt），y2=3cos（100πt），则这两个声波合成后即y=y1+y2的振幅为（　　）
A、3
B、6
C、3
2
D、6
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网