题目内容
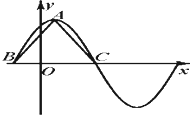设函数f（x）=[2sin（ωx+| π |
| 4 |
| 2 |
| 2 |
（Ⅰ）求ω的值及函数f（x）的值域；
（Ⅱ）若f（x0）=
| 13 |
| 7 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：（Ⅰ）由条件求得f（x）=2sin（2ωx+
），求得BC=4，可得函数的周期为8，由此求得ω的值以及函数的值域．
（Ⅱ）由条件求得sin(
x0+
)=
，由x0∈（1，3），可得
x0+
∈(
，π)，求得cos(
x0+
)=-
．再由f（x0-1）=2sin[（
x0+
）-
]利用两角差的正弦公式计算求得结果．
| π |
| 4 |
（Ⅱ）由条件求得sin(
| π |
| 4 |
| π |
| 4 |
| 13 |
| 14 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
3
| ||
| 14 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答：
解：（Ⅰ）由题意可得f(x)=
sin2ωx+
cos2ωx=2sin(2ωx+
)，
∵A为图象最高点，△ABC为等腰直角三角形，∴BC=4，故函数的周期为8，
∴
=8，∴ω=
，∴f（x）=2sin（
x+
），且f（x）的值域为[-2，2]．
（Ⅱ）若f（x0）=
，即sin(
x0+
)=
，
∵x0∈（1，3），∴
x0+
∈(
，π)，∴cos(
x0+
)=-
．
∴f（x0-1）=2sin[
（x0-1）+
]=2sin
x0=2sin[（
x0+
）-
]
=2sin（
x0+
）cos
-2cos（
x0+
）sin
=2×
×
-2×（-
）×
=
．
| 2 |
| 2 |
| π |
| 4 |
∵A为图象最高点，△ABC为等腰直角三角形，∴BC=4，故函数的周期为8，
∴
| 2π |
| 2ω |
| π |
| 8 |
| π |
| 4 |
| π |
| 4 |
（Ⅱ）若f（x0）=
| 13 |
| 7 |
| π |
| 4 |
| π |
| 4 |
| 13 |
| 14 |
∵x0∈（1，3），∴
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
3
| ||
| 14 |
∴f（x0-1）=2sin[
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=2sin（
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 13 |
| 14 |
| ||
| 2 |
3
| ||
| 14 |
| ||
| 2 |
13
| ||||
| 14 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，同角三角函数的基本关系、两角差的正弦公式的应用，属于基础题．
练习册系列答案
相关题目
对于线性相关系数r，叙述正确的是（ ）
| A、r∈（-∞，+∞），|r|越大，相关程度越大，反之相关程度越小 |
| B、r∈（-∞，+∞），r越大，相关程度越大，反之相关程度越小 |
| C、|r|≤1且|r|越接近1，相关程度越大 |
| D、以上说法都不对 |
