题目内容
已知函数f(x)=log
|sinx|.
(1)求其定义域和值域;
(2)判断其奇偶性;
(3)求其周期;
(4)写出单调区间.
| 1 |
| 2 |
(1)求其定义域和值域;
(2)判断其奇偶性;
(3)求其周期;
(4)写出单调区间.
考点:正弦函数的奇偶性
专题:计算题,函数的性质及应用,三角函数的图像与性质
分析:(1)由|sinx|>0得sinx≠0,即x≠kπ(k∈Z),即可得到定义域;由0<|sinx|≤1,运用对数函数的单调性,即可得到值域;
(2)运用奇偶性的定义和诱导公式,即可判断,注意定义域关于原点对称;
(3)运用周期函数的定义,计算得到f(x+π)=f(x),即可判断;
(4)令u=|sinx|,则y=log
u在(0,+∞)上是减函数,求出u=|sinx|的单调区间,再由复合函数的单调性:同增异减,即可得到.
(2)运用奇偶性的定义和诱导公式,即可判断,注意定义域关于原点对称;
(3)运用周期函数的定义,计算得到f(x+π)=f(x),即可判断;
(4)令u=|sinx|,则y=log
| 1 |
| 2 |
解答:
解:(1)由|sinx|>0得sinx≠0,∴x≠kπ(k∈Z).
即函数定义域为{x∈R|x≠kπ,k∈Z}.
又0<|sinx|≤1,∴log
|sinx|≥0.
∴函数的值域为[0,+∞).
(2)∵f(x)的定义域关于原点对称,
且f(-x)=)=log
|sin(-x)|=log
|sinx|=f(x).
∴f(x)为偶函数.
(3)函数f(x)是周期函数,
∵f(x+π)=log
|sin(x+π)|=log
|sinx|=f(x),
∴f(x)的周期T=π.
(4)令u=|sinx|,
则y=log
u在(0,+∞)上是减函数,
由于u在(kπ,kπ+
)上递增,在(kπ+
,kπ+π)上递减,
则f(x)在(kπ,kπ+
)上递减,在(kπ+
,kπ+π)上递增,
即f(x)的单调增区间为(kπ+
,kπ+π),单调减区间为(kπ,kπ+
)(k∈Z).
即函数定义域为{x∈R|x≠kπ,k∈Z}.
又0<|sinx|≤1,∴log
| 1 |
| 2 |
∴函数的值域为[0,+∞).
(2)∵f(x)的定义域关于原点对称,
且f(-x)=)=log
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)为偶函数.
(3)函数f(x)是周期函数,
∵f(x+π)=log
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)的周期T=π.
(4)令u=|sinx|,
则y=log
| 1 |
| 2 |
由于u在(kπ,kπ+
| π |
| 2 |
| π |
| 2 |
则f(x)在(kπ,kπ+
| π |
| 2 |
| π |
| 2 |
即f(x)的单调增区间为(kπ+
| π |
| 2 |
| π |
| 2 |
点评:本题考查函数的性质及运用,考查函数的定义域和值域,函数的奇偶性,注意定义域关于原点对照,函数的周期性和函数的单调性,注意复合函数的单调性:同增异减,属于中档题和易错题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若a>b,x>y,则下列不等式中正确的是( )
| A、a-x>b-y | ||||
| B、ax>by | ||||
C、
| ||||
| D、x-b>y-a |
若(x-
)n的展开式中第3项的二项式系数是10,则展开式中所有项系数之和为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 设函数f(x)=[2sin(ωx+
设函数f(x)=[2sin(ωx+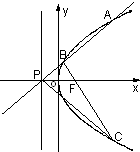 已知曲线W上的动点M到点F(1,0)的距离等于它到直线x=-1x=-1的距离.过点P(-1,0)任作一条直线l与曲线W交于不同的两点A、B,点A关于x轴的对称点为C.
已知曲线W上的动点M到点F(1,0)的距离等于它到直线x=-1x=-1的距离.过点P(-1,0)任作一条直线l与曲线W交于不同的两点A、B,点A关于x轴的对称点为C.