题目内容
11.设函数f(x)=2sinxcos2$\frac{φ}{2}$+cosxsinφ-sinx(0<φ<π)在x=π处取最小值.(I)求ϕ的值,并化简f(x);
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,已知a=1,b=$\sqrt{2}$,f(A)=$\frac{{\sqrt{3}}}{2}$,求角C.
分析 (I)由条件利用三角恒等变换,化简函数的解析式,再利用诱导公式求得φ的值,可得函数的解析式.
(II)由条件求得A,再利用正弦定理求得sinB的值,可得B,再利用三角形内角和公式求得C的值.
解答 解:(I)∵$f(x)=2sinx•\frac{1+cosφ}{2}+cosxsinφ-sinx$=sinx+sinxcosφ+cosxsinφ-sinx
=sinxcosφ+cosxsinφ=sin(x+φ),
因为函数f (x)在x=π处取最小值,所以sin(π+φ)=-1,
由诱导公式知sinφ=1,因为0<φ<π,所以$φ=\frac{π}{2}$,所以$f(x)=sin(x+\frac{π}{2})=cosx$.
(II)因为$f(A)=\frac{{\sqrt{3}}}{2}$,所以$cosA=\frac{{\sqrt{3}}}{2}$,因为角A为△ABC的内角,所以$A=\frac{π}{6}$.
又因为$a=1,b=\sqrt{2}$,所以由正弦定理,得$\frac{a}{sinA}=\frac{b}{sinB}$,
也就是$sinB=\frac{bsinA}{a}=\sqrt{2}×\frac{1}{2}=\frac{{\sqrt{2}}}{2}$,
因为b>a,所以$B=\frac{π}{4}$或$B=\frac{3π}{4}$.
当$B=\frac{π}{4}$时,$C=π-\frac{π}{6}-\frac{π}{4}=\frac{7π}{12}$;
当$B=\frac{3π}{4}$时,$C=π-\frac{π}{6}-\frac{3π}{4}=\frac{π}{12}$.
点评 本题主要考查三角恒等变换,诱导公式的应用,正弦定理以及三角形的内角和公式,属于基础题.

 优百分课时互动系列答案
优百分课时互动系列答案| 课程 人数 | 数学 | 英语 | 物理 | 化学 |
| 100 | √ | × | √ | √ |
| 217 | × | √ | × | √ |
| 200 | √ | √ | √ | × |
| 300 | √ | × | √ | × |
| 85 | √ | × | × | × |
| 98 | × | √ | × | × |
(1)估计当地某一学生同时参加英语和物理培训的概率;
(2)估计当地某一学生在以上四门课程同时参加三门培训的概率;
(3)如果一个学生参加了数学培训,则该生同时参加英语、物理、化学培训中哪一种的可能性最大?说明理由.
①从10盒黑色水笔芯中抽取2盒进行质量检查.
②天空影院有32排,每排有60个座位,《速度与激情7》首映当晚,恰好坐满了观众,电影结束后,为了听取意见,需要请32名观众进行座谈.
③抚州市某中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,拟抽取一个容量为20的样本.
请问较为合理的抽样方法是( )
| A. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| B. | ①简单随机抽样,②分层抽样,③系统抽样 | |
| C. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| D. | ①分层抽样,②系统抽样,③简单随机抽样 |
| A. | 向左平移$\frac{π}{8}$个单位长度 | B. | 向右平移$\frac{π}{8}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
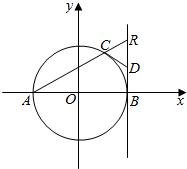 已知A(-3,0),B(3,0),C(x0,y0)是圆M上的三个不同的点.
已知A(-3,0),B(3,0),C(x0,y0)是圆M上的三个不同的点.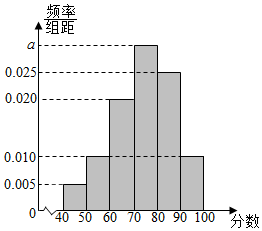 某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.
某校从高二年级学生中随机抽取40名学生,将他们的期中考试政治成绩(满分100分,成绩均不低于40分的整数)分成六段:[40,50),[50,60),[60,70),[70,80)[80,90),[90,100]后,得到如图所示的频率分布直方图.
 如图所示,E,F分别是正方体ABCD-A1B1C1D1中BB1,B1C1的中点,计算:
如图所示,E,F分别是正方体ABCD-A1B1C1D1中BB1,B1C1的中点,计算: