题目内容
1. 已知A(-3,0),B(3,0),C(x0,y0)是圆M上的三个不同的点.
已知A(-3,0),B(3,0),C(x0,y0)是圆M上的三个不同的点.(1)若x0=-4,y0=1,求圆M的方程;
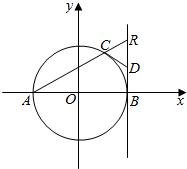
(2)若点C是以AB为直径的圆M上的任意一点,直线x=3交直线AC于点R,线段BR的中点为D.判断直线CD与圆M的位置关系,并证明你的结论.
分析 (1)利用待定系数法建立方程关系进行求解即可.
(2)根据直线和圆的位置关系进行判断即可.
解答  解:(1)设圆的方程为x2+y2+Dx+Ey+F=0$\left\{\begin{array}{l}9-3D+F=0\\ 9-3D+F=0\\ 17-4D+E+F=0\end{array}\right.⇒\left\{\begin{array}{l}D=0\\ E=-8\\ F=-9\end{array}\right.$
解:(1)设圆的方程为x2+y2+Dx+Ey+F=0$\left\{\begin{array}{l}9-3D+F=0\\ 9-3D+F=0\\ 17-4D+E+F=0\end{array}\right.⇒\left\{\begin{array}{l}D=0\\ E=-8\\ F=-9\end{array}\right.$
圆的方程为x2+y2-8y-9=0…(6分)
(2)直线CD与圆M相切O、D分别是AB、BR的中点
则OD∥AR,∴∠CAB=∠DOB,∠ACO=∠COD,
又∠CAO=∠ACO,∴∠DOB=∠COD
又OC=OB,所以△BOD≌△COD
∴∠OCD=∠OBD=90°
即OC⊥CD,则直线CD与圆M相切. …(12分)
(其他方法亦可)
点评 本题主要考查圆的一般方程的求解以及直线和圆的位置关系的判断,利用待定系数法求出圆的方程是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.“x2=y2”是“x=y”的( )
| A. | 充分不必要条件 | B. | 充分必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
12.已知m,n表示两条不同直线,α表示平面,下列说法正确的是( )
| A. | 若m⊥α,n?α,则m⊥n | B. | 若m⊥α,m⊥n,则n∥α | C. | 若m∥α,m⊥n,则n⊥α | D. | 若m∥α,n∥α,则m∥n |
13.下列函数中,不是奇函数的是( )
| A. | y=1-x2 | B. | y=tanx | C. | y=sin2x | D. | y=5x-5-x |