题目内容
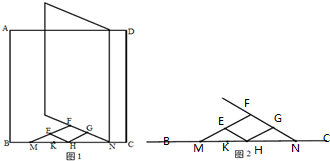 如图1是某窗户的窗扣示意图,图2是其俯视图,其中点E、F、G、M、K是固定点,点H是窗沿糟内可滑动点,点N是窗户下边沿延长线与窗沿的交点,窗户打开时,点H、N向点K移动,当点H移至点K时,不能再往左移动,此时窗户最大打开,窗户关闭时,点H、N向点C移动,当点N移动至点C时,点E、F、G落在BC上窗户刚好全部关闭.在窗户打开与关闭的过程中,四边形EFGH始终保持平行四边形的形状,现测得BM=18cm,MK=12cm,ME=EF,FG=GN,且HE=6cm,HG=10cm;
如图1是某窗户的窗扣示意图,图2是其俯视图,其中点E、F、G、M、K是固定点,点H是窗沿糟内可滑动点,点N是窗户下边沿延长线与窗沿的交点,窗户打开时,点H、N向点K移动,当点H移至点K时,不能再往左移动,此时窗户最大打开,窗户关闭时,点H、N向点C移动,当点N移动至点C时,点E、F、G落在BC上窗户刚好全部关闭.在窗户打开与关闭的过程中,四边形EFGH始终保持平行四边形的形状,现测得BM=18cm,MK=12cm,ME=EF,FG=GN,且HE=6cm,HG=10cm;(1)求窗户的宽BC的长;
(2)求线段HC的长的取值范围;
(3)求窗户张角∠MNF的最大值(结果精确到0.1)(参考数据:sin56.2°≈0.831,cos56.2°≈0.556,tan56.2°≈1.494可使用科学计算器).
考点:函数的值,函数解析式的求解及常用方法
专题:函数的性质及应用
分析:(1)由于四边形EFGH始终保持平行四边形的形状,再利用三角形的中位线定理即可得出;
(2)利用
MC≤HC≤KC=BC-BK即可得出;
(3)当H移到K时,MN最短为2MK=24,最长为MC=32.当MN取最短24时,∠MNF取得最大角,利用余弦定理即可得出.
(2)利用
| 1 |
| 2 |
(3)当H移到K时,MN最短为2MK=24,最长为MC=32.当MN取最短24时,∠MNF取得最大角,利用余弦定理即可得出.
解答:
解:(1)∵四边形EFGH始终保持平行四边形的形状,ME=EF,FG=GN,且HE=6cm,HG=10cm,
∴MC=MF+FC=2HG+2EH=2×(6+10)=32.
∴BC=BM+MC=18+32=50cm.
(2)∵16=
MC≤HC≤KC=BC-BK=50-(18+12)=20,
∴HC∈[16,20].
(3)当H移到K时,MN最短为2MK=24,最长为MC=32.
当MN取最短24时,∠MNF取得最大角,cos∠MNF=
=
≈0.556.
∴∠MNF≈56.2°.
∴MC=MF+FC=2HG+2EH=2×(6+10)=32.
∴BC=BM+MC=18+32=50cm.
(2)∵16=
| 1 |
| 2 |
∴HC∈[16,20].
(3)当H移到K时,MN最短为2MK=24,最长为MC=32.
当MN取最短24时,∠MNF取得最大角,cos∠MNF=
| 242+122-202 |
| 2×24×12 |
| 5 |
| 9 |
∴∠MNF≈56.2°.
点评:本题考查了平行四边形的性质、三角形的中位线定理、余弦定理,考查了推理能力与计算能力,属于较难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
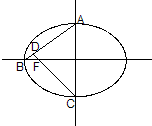 已知如图,椭圆的离心率为
已知如图,椭圆的离心率为| 1 |
| 2 |
A、-3
| ||
B、3-
| ||
C、3
| ||
D、3+
|