题目内容
函数f（x）=|x-m|+|x+3|的图象与直线y=2有公共点，则m的取值范围是 ．
考点：绝对值不等式的解法
专题：函数的性质及应用,不等式的解法及应用
分析：利用不等式的性质将函数解析式的最小值利用m表示出来，然后只要|m+3|≤2，解此绝对值不等式．
解答：
解：∵|x-m|+|x+3|≥|x-m-x-3|=|m+3|，
∴要使函数f（x）=|x-m|+|x+3|的图象与直线y=2有公共点，
只要|m+3|≤2，
解得-5≤m≤-1；
故答案为：-5≤m≤-1．
∴要使函数f（x）=|x-m|+|x+3|的图象与直线y=2有公共点，
只要|m+3|≤2，
解得-5≤m≤-1；
故答案为：-5≤m≤-1．
点评：本题考查了三角不等式的运用以及绝对值不等式的解法；关键是得到函数的最小值，然后解不等式．
练习册系列答案
手拉手全优练考卷系列答案
相关题目
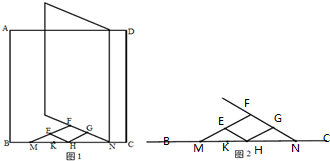如图1是某窗户的窗扣示意图，图2是其俯视图，其中点E、F、G、M、K是固定点，点H是窗沿糟内可滑动点，点N是窗户下边沿延长线与窗沿的交点，窗户打开时，点H、N向点K移动，当点H移至点K时，不能再往左移动，此时窗户最大打开，窗户关闭时，点H、N向点C移动，当点N移动至点C时，点E、F、G落在BC上窗户刚好全部关闭．在窗户打开与关闭的过程中，四边形EFGH始终保持平行四边形的形状，现测得BM=18cm，MK=12cm，ME=EF，FG=GN，且HE=6cm，HG=10cm；