题目内容
已知二次函数f（x）=ax2+4x+3a，且f（1）=0，求：
（1）函数f（x）零点的个数；
（2）函数f（x）在[t，t+1]上的最大值．
（1）函数f（x）零点的个数；
（2）函数f（x）在[t，t+1]上的最大值．
考点：二次函数在闭区间上的最值,根的存在性及根的个数判断
专题：函数的性质及应用
分析：（1）由f（1）=0求得a=-1，可得 f（x）=-（x-1）（x-3），由此可得函数f（x）零点的个数．
（2）由于f（x）=-（x-2）2+1，它的图象的对称轴方程为x=2，再分对称轴在区间[t，t+1]左侧、右侧、中间三种情况，分别利用二次函数的性质求得它的最大值．
当t＞2时，函数f（x）在[t，t+1]上是减函数，函数的最大值为f（t）=-t2+4t+-3；
当t+1＜2时，函数f（x）在[t，t+1]上是增函数，函数的最大值为f（t+1）=-（t+1）2+4（t+1）-3=-t2+2t；
当2∈[t，t+1]时，函数的最大值
（2）由于f（x）=-（x-2）2+1，它的图象的对称轴方程为x=2，再分对称轴在区间[t，t+1]左侧、右侧、中间三种情况，分别利用二次函数的性质求得它的最大值．
当t＞2时，函数f（x）在[t，t+1]上是减函数，函数的最大值为f（t）=-t2+4t+-3；
当t+1＜2时，函数f（x）在[t，t+1]上是增函数，函数的最大值为f（t+1）=-（t+1）2+4（t+1）-3=-t2+2t；
当2∈[t，t+1]时，函数的最大值
解答：
解：（1）∵二次函数f（x）=ax2+4x+3a，且f（1）=0，∴4a+4=1，∴a=-1，
∴f（x）=-x2+4x+-3=-（x-1）（x-3），故函数f（x）零点的个数为2．
（2）由于f（x）=-x2+4x+-3=-（x-2）2+1，它的图象的对称轴方程为x=2，
当t＞2时，函数f（x）在[t，t+1]上是减函数，函数的最大值为f（t）=-t2+4t+-3；
当t+1＜2时，函数f（x）在[t，t+1]上是增函数，函数的最大值为f（t+1）=-（t+1）2+4（t+1）-3=-t2+2t；
当2∈[t，t+1]时，函数的最大值为f（2）=1．
∴f（x）=-x2+4x+-3=-（x-1）（x-3），故函数f（x）零点的个数为2．
（2）由于f（x）=-x2+4x+-3=-（x-2）2+1，它的图象的对称轴方程为x=2，
当t＞2时，函数f（x）在[t，t+1]上是减函数，函数的最大值为f（t）=-t2+4t+-3；
当t+1＜2时，函数f（x）在[t，t+1]上是增函数，函数的最大值为f（t+1）=-（t+1）2+4（t+1）-3=-t2+2t；
当2∈[t，t+1]时，函数的最大值为f（2）=1．
点评：本题主要考查求二次函数在闭区间上的最值，二次函数的性质的应用，体现了分类讨论的数学思想，属基础题．
练习册系列答案
相关题目
已知函数f（x）满足f（x）=f（-x），且当x∈（-∞，0），f（x）+xf′（x）＜0成立，若a=（20.1）•f（20.1），b=（ln2）•f（ln2），c=（log2
）•f（log2
），则a，b，c的大小关系是（ ）
| 1 |
| 8 |
| 1 |
| 8 |
| A、a＞b＞c |
| B、c＞b＞a |
| C、c＞a＞b |
| D、a＞c＞b |
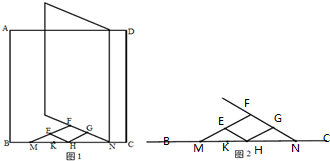如图1是某窗户的窗扣示意图，图2是其俯视图，其中点E、F、G、M、K是固定点，点H是窗沿糟内可滑动点，点N是窗户下边沿延长线与窗沿的交点，窗户打开时，点H、N向点K移动，当点H移至点K时，不能再往左移动，此时窗户最大打开，窗户关闭时，点H、N向点C移动，当点N移动至点C时，点E、F、G落在BC上窗户刚好全部关闭．在窗户打开与关闭的过程中，四边形EFGH始终保持平行四边形的形状，现测得BM=18cm，MK=12cm，ME=EF，FG=GN，且HE=6cm，HG=10cm；