题目内容
9.将边长为2的正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,则三棱锥C-ABD的外接球表面积为( )| A. | 16π | B. | 12π | C. | 8π | D. | 4π |
分析 根据题意,画出图形,结合图形得出三棱锥C-ABD的外接球直径,从而求出外接球的表面积.
解答 解:将边长为2的正方形ABCD沿对角线BD折起,得到三棱锥C-ABD,
如图所示:
则BC⊥CD,BA⊥AD;
三棱锥C-ABD的外接球直径为BD=2$\sqrt{2}$,
外接球的表面积为4πR2=${(2\sqrt{2})}^{2}$π=8π.
故选:C.
点评 本题考查了平面图形的折叠问题,也考查了空间想象能力的应用问题,是基础题目.

练习册系列答案
相关题目
17.已知A为锐角,$lg(\frac{1}{1+cosA})=m,lg(1-cosA)=n$,则lgsinA的值是( )
| A. | m-$\frac{1}{n}$ | B. | n-m | C. | $\frac{1}{2}$(m-$\frac{1}{n}$) | D. | $\frac{1}{2}$(n-m) |
14.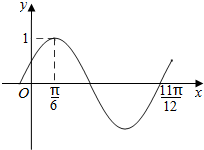 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
18.设等差数列{an}满足a3=5,a10=-9.则{an}的前n项和Sn取得最大值是( )
| A. | 23 | B. | 25 | C. | 27 | D. | 29 |
19.设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2016(x)=( )
| A. | sinx | B. | -sinx | C. | cosx | D. | -cosx |
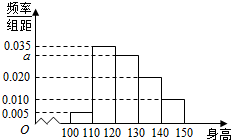 从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取36人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为( )
从某小学随机抽取200名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取36人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为( )