题目内容
8.下列函数中,最小正周期为π,且在[$\frac{π}{3}$,$\frac{5π}{6}$]上是减函数的是( )| A. | y=sin(2x-$\frac{π}{3}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=sin(2x+$\frac{π}{6}$) | D. | y=sin($\frac{1}{2}$x+$\frac{π}{6}$) |
分析 由周期为π及减区间长度为半周期可知函数在区间端点取得最值.
解答 解:∵函数的最小正周期T=π,在[$\frac{π}{3}$,$\frac{5π}{6}$]上是减函数,且区间[$\frac{π}{3}$,$\frac{5π}{6}$]的区间长度为$\frac{5π}{6}-\frac{π}{3}$=$\frac{π}{2}$=$\frac{T}{2}$.
∴该函数在x=$\frac{π}{3}$时取得最大值,在x=$\frac{5π}{6}$时取得最小值.
对于A,当x=$\frac{π}{3}$时,y=sin$\frac{π}{3}$,不符合要求;
对于B,当x=$\frac{π}{3}$时,y=sin$\frac{π}{2}$=1,当x=$\frac{5π}{6}$时,y=sin$\frac{3π}{2}$=-1,符合要求.
对于C,当x=$\frac{π}{3}$时,y=sin$\frac{5π}{6}$,不符合要求;
对于D,周期T=$\frac{2π}{\frac{1}{2}}$=4π,不符合要求.
故选B.
点评 本题考查了三角函数的图象与性质,属于基础题.

练习册系列答案
相关题目
18.p:5是15的约数; q:π是有理数 则( )
| A. | p∧q是真命题 | B. | p∨q是假命题 | C. | ¬p是真命题 | D. | ¬q是真命题 |
3.某几何体的三视图如图所示,若该几何体的体积等于16+8π,则r等于( )
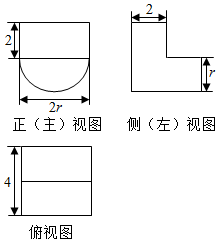

| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |