题目内容
16.设抛物线C:y2=4x的焦点为F,过F的直线l与抛物线交于A,B两点,M为抛物线C的准线与x轴的交点,若tan∠AMB=2$\sqrt{2}$,则|AB|=8.分析 设AB方程y=k(x-1),与抛物线方程y2=4x联立,利用tan∠AMB=2$\sqrt{2}$,建立k的方程,即可得出结论..
解答 解:焦点F(1,0),M(-1,0),设AB方程y=k(x-1),
设A(x1,y1),B(x2,y2)
∵tan∠AMB=2$\sqrt{2}$,
∴$\frac{\frac{{y}_{1}}{{x}_{1}+1}-\frac{{y}_{2}}{{x}_{2}+1}}{1+\frac{{y}_{1}}{{x}_{1}+1}•\frac{{y}_{2}}{{x}_{2}+1}}$=2$\sqrt{2}$,
整理可得2k(x1-x2)=2$\sqrt{2}$(x1+1)(x2+1)+2$\sqrt{2}$y1y2…(*)
y=k(x-1),与y2=4x联立可得k2x2-(2k2+4)x+k2=0
可得x1x2=$\frac{1}{4}$p2=1,x1+x2=$\frac{4}{{k}^{2}}$+2,y1y2=-p2=-4
代入(*)可得2k(x1-x2)=2$\sqrt{2}$($\frac{4}{{k}^{2}}$),∴x1-x2=$\frac{4\sqrt{2}}{{k}^{3}}$,
∴($\frac{4}{{k}^{2}}$+2)2-4=($\frac{4\sqrt{2}}{{k}^{3}}$)2,
∴k=±1,
∴x1+x2=$\frac{4}{{k}^{2}}$+2=6,
∴|AB|=$\sqrt{1+1}•\sqrt{36-4}$=8
故答案为:8.
点评 本题考查直线与抛物线的位置关系,考查差角的正切公式,正确运用韦达定理是关键.

练习册系列答案
相关题目
1.l与抛物线y2=2px相交于A、B两点,O为原点,如果0A垂直于0B,则l一定过( )
| A. | ($\frac{p}{2}$,0) | B. | (p,0) | C. | (2p,0) | D. | (3p,0) |
8.下列函数中,最小正周期为π,且在[$\frac{π}{3}$,$\frac{5π}{6}$]上是减函数的是( )
| A. | y=sin(2x-$\frac{π}{3}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=sin(2x+$\frac{π}{6}$) | D. | y=sin($\frac{1}{2}$x+$\frac{π}{6}$) |
5.定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{|x-3|-1,x>1}\\{lo{g}_{2}(x+1),0≤x≤1}\end{array}\right.$则函数g(x)=f(x)-m(0<m<1)的所有零点之和为( )
| A. | 1-2m | B. | 2m-1 | C. | 1-($\frac{1}{2}$)m | D. | ($\frac{1}{2}$)m-1 |
 函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,且A>0,ω>0)的部分图象如图所示,下列结论:
函数f(x)=Asin(ωx+ϕ)(A,ω,ϕ是常数,且A>0,ω>0)的部分图象如图所示,下列结论: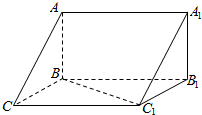 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,BC1=$\sqrt{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,BC1=$\sqrt{3}$.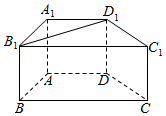 如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=AD=AA1=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°.
如图,四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,AB=AD=AA1=2.底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,∠BCD=45°.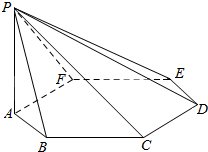 设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求
设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求