题目内容
17.设函数f(x)=sinx(sinx+$\sqrt{3}$cosx),x∈R.(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间[-$\frac{π}{4}$,$\frac{π}{6}$]上的值域.
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=sin(2x-$\frac{π}{6}$)$+\frac{1}{2}$,利用周期公式即可得解.
(2)由范围x∈[-$\frac{π}{4}$,$\frac{π}{6}$],可求2x-$\frac{π}{6}$∈[-$\frac{2π}{3}$,$\frac{π}{6}$],利用正弦函数的图象和性质即可得解值域.
解答 解:(1)∵f(x)=sinx(sinx+$\sqrt{3}$cosx)
=sin2x+$\sqrt{3}$sinxcosx
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$cos2x+$\frac{1}{2}$
=sin(2x-$\frac{π}{6}$)$+\frac{1}{2}$,
∴函数f(x)的最小正周期T=$\frac{2π}{2}=π$.
(2)∵x∈[-$\frac{π}{4}$,$\frac{π}{6}$],
∴2x-$\frac{π}{6}$∈[-$\frac{2π}{3}$,$\frac{π}{6}$],
∴sin(2x-$\frac{π}{6}$)∈[-1,$\frac{1}{2}$],
∴函数f(x)=sin(2x-$\frac{π}{6}$)$+\frac{1}{2}$在区间[-$\frac{π}{4}$,$\frac{π}{6}$]上的值域为:[-$\frac{1}{2}$,1].
点评 本题值域考查了三角函数恒等变换的应用,正弦函数的图象和性质,三角函数周期公式的应用,属于基础题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
8.下列函数中,最小正周期为π,且在[$\frac{π}{3}$,$\frac{5π}{6}$]上是减函数的是( )
| A. | y=sin(2x-$\frac{π}{3}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=sin(2x+$\frac{π}{6}$) | D. | y=sin($\frac{1}{2}$x+$\frac{π}{6}$) |
5.定义在R上的奇函数f(x),当x≥0时,f(x)=$\left\{\begin{array}{l}{|x-3|-1,x>1}\\{lo{g}_{2}(x+1),0≤x≤1}\end{array}\right.$则函数g(x)=f(x)-m(0<m<1)的所有零点之和为( )
| A. | 1-2m | B. | 2m-1 | C. | 1-($\frac{1}{2}$)m | D. | ($\frac{1}{2}$)m-1 |
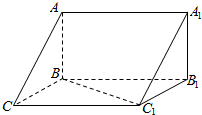 如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,BC1=$\sqrt{3}$.
如图,在三棱柱ABC-A1B1C1中,已知AB⊥侧面BB1C1C,BC=1,CC1=2,BC1=$\sqrt{3}$.