题目内容
3.某几何体的三视图如图所示,若该几何体的体积等于16+8π,则r等于( )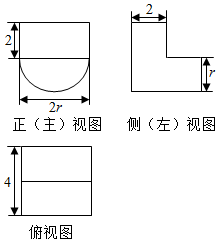
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
分析 几何体为长方体与半圆柱的组合体.根据体积列方程解出r.
解答 解:由三视图可知几何体为长方体与半圆柱的组合体.
长方体的长宽高分别是2r,2,2,半圆柱的底面半径为r,高为4.
∴几何体的体积V=2r×2×2+$\frac{1}{2}×π×{r}^{2}×4$=16+8π.
解得r=2.
故选B.
点评 本题考查了常见几何体的三视图,结构特征,体积计算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知双曲线的渐近线方程为$y=±\sqrt{2}x$,焦点坐标为$(0,-\sqrt{6})$、$(0,\sqrt{6})$,则双曲线方程为( )
| A. | $\frac{y^2}{2}-\frac{x^2}{8}=1$ | B. | $\frac{y^2}{8}-\frac{x^2}{2}=1$ | C. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | D. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ |
14.已知函数f(x)的图象是连续不间断的,且有如下的x,f(x)对应值表:
则函数f(x)在区间[1,6]上的零点有( )
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 11.8 | 8.6 | -6.4 | 4.5 | -26.8 | -86.2 |
| A. | 2个 | B. | 3个 | C. | 至少3个 | D. | 至多2个 |
8.下列函数中,最小正周期为π,且在[$\frac{π}{3}$,$\frac{5π}{6}$]上是减函数的是( )
| A. | y=sin(2x-$\frac{π}{3}$) | B. | y=sin(2x-$\frac{π}{6}$) | C. | y=sin(2x+$\frac{π}{6}$) | D. | y=sin($\frac{1}{2}$x+$\frac{π}{6}$) |
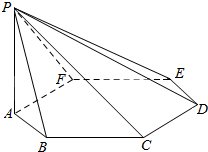 设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求
设ABCDEF是边长为1的正六边形,PA垂直于正六边形所在的平面,且PA=2.求