题目内容
7.设函数f(x)=|x-4|,g(x)=|2x+1|.(1)解不等式f(x)<g(x);
(2)若2f(x)+g(x)>ax对任意的实数x恒成立,求a的取值范围.
分析 (1)f(x)<g(x)等价于(x-4)2<(2x+1)2,从而求得不等式f(x)<g(x)的解集.
(2)由题意2f(x)+g(x)>ax对任意的实数x恒成立,即H(x)的图象恒在直线G(x)=ax的上,即可求得a的范围.
解答 解:(1)f(x)<g(x)等价于(x-4)2<(2x+1)2,∴x2+4x-5>0,
∴x<-5或x>1,
∴不等式的解集为{x|x<-5或x>1};
(2)令H(x)=2f(x)+g(x)=$\left\{\begin{array}{l}{4x-7,x>4}\\{9,-\frac{1}{2}≤x≤4}\\{-4x+7,x<-\frac{1}{2}}\end{array}\right.$,G(x)=ax,
2f(x)+g(x)>ax对任意的实数x恒成立,即H(x)的图象恒在直线G(x)=ax的上方.
故直线G(x)=ax的斜率a满足-4≤a<$\frac{9}{4}$,即a的范围为[-4,$\frac{9}{4}$).
点评 本题主要考查绝对值的意义,带由绝对值的函数,函数的恒成立问题,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
18.从1,2,3,4,5中任意取出两个不同的数,则这两个数不相邻的概率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
15.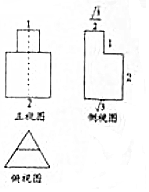 已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )
已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )
 已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )
已知一个几何体的三视图如图所示(正视图是两个正方形,俯视图是两个正三角形),则其体积为( )| A. | $\frac{{3\sqrt{3}}}{2}$ | B. | $\frac{{9\sqrt{3}}}{4}$ | C. | $3\sqrt{3}$ | D. | $\frac{{9\sqrt{3}}}{2}$ |
6.已知点(a,b)是圆x2+y2=r2外的一点,则直线ax+by=r2与圆的位置关系 ( )
| A. | 相离 | B. | 相切 | C. | 相交且不过圆心 | D. | 相交且过圆心 |