题目内容
在△ABC中，E、F分别为AB、AC中点，P为EF的中点，实数x、y满足
+x
+y
=
，则2x+y的值为（ ）
| PA |
| PB |
| PC |
| 0 |
| A、-1 | ||
| B、1 | ||
C、-
| ||
D、
|
考点：向量加减混合运算及其几何意义
专题：平面向量及应用
分析：如图所示，以PB，PC为邻边作平行四边形PBNC，连接对角线PN与BC相较于点M．由于E、F分别为AB、AC中点，P为EF的中点，可得
+
=
=2
=-2
，化为
+
+
=
．与已知
+x
+y
=
比较即可得出．
| PB |
| PC |
| PN |
| PM |
| PA |
| PA |
| 1 |
| 2 |
| PB |
| 1 |
| 2 |
| PC |
| 0 |
| PA |
| PB |
| PC |
| 0 |
解答：
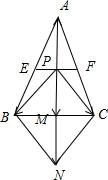解：如图所示，
以PB，PC为邻边作平行四边形PBNC，连接对角线PN与BC相较于点M．
∵E、F分别为AB、AC中点，P为EF的中点，
∴
+
=
=2
=-2
，
∴
+
+
=
．
又实数x、y满足
+x
+y
=
，
∴x=
=y．
∴2x+y=2×
+
=
．
故选：D．
解：如图所示，以PB，PC为邻边作平行四边形PBNC，连接对角线PN与BC相较于点M．
∵E、F分别为AB、AC中点，P为EF的中点，
∴
| PB |
| PC |
| PN |
| PM |
| PA |
∴
| PA |
| 1 |
| 2 |
| PB |
| 1 |
| 2 |
| PC |
| 0 |
又实数x、y满足
| PA |
| PB |
| PC |
| 0 |
∴x=
| 1 |
| 2 |
∴2x+y=2×
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选：D．
点评：本题考查了向量的平行四边形法则、向量共线定理、向量的基本定理等基础知识与基本技能方法，考查了推理能力，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
相关题目
5个同学排成一排照相，要求甲乙两同学相邻，则不同的排法种法是（ ）
| A、36 | B、48 | C、72 | D、120 |
已知函数g（x）=2-3x，f（g（x））=
，则f（
）=（ ）
| 3x |
| x2-1 |
| 1 |
| 2 |
| A、-2 | ||
B、
| ||
| C、-15 | ||
| D、30 |
集合A={x|x2-2x=0}B={-1，0，1}，则A∩B=（ ）
| A、{0，2} | B、{2} |
| C、{0} | D、{0，1} |
在复平面内，复数
对应的点位于（ ）
| 2 |
| 1-i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知集合M={x|
＞0}，N={x|x≤-3}，则{x|x≥1}等于（ ）
| x+3 |
| 1-x |
| A、（∁RM）∩N |
| B、M∪（∁RN） |
| C、∁R（M∩N） |
| D、∁R（M∪N） |
若角α的终边过点（-1，2），则cos2α的值为（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|