题目内容
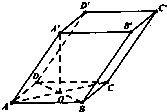 如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=
如图四棱柱ABCD-A′B′C′D′的底面是正方形,O是底面的中心,A′O=1,AB=AA′=A′D=A′B=| 2 |
(1)证明:平面A′BD∥平面B′CD′;
(2)求三棱锥C-ADD′的体积VC-ADD′.
考点:平面与平面平行的判定,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)由已知条件推导出A′BCD′是平行四边形,从而得到A′B∥面B′CD′,由此能够证明平面A′BD∥平面B′CD′.
(2)先证明A′O⊥平面ABCD,再求三棱锥C-ADD′的体积VC-ADD′.
(2)先证明A′O⊥平面ABCD,再求三棱锥C-ADD′的体积VC-ADD′.
解答:
(1)证明:在四棱柱中,
∵BC∥A′D′,且BC=A′D′,
∴A′BCD′是平行四边形,
∴A′B∥CD′,
又∵A′B?平面B′CD′,CD′?B′CD′,
∴A′B∥面B′CD′,
又A′B?面A′BD,A′D?面A′BD,且A′B∩A′D=A′,
∴平面A′BD∥平面B′CD′.
(2)解:∵A′O=1,AB=AA′=A′D=
.
∴A′O2+OA2=AA'2,A′O2+OB2=A′B2,
∴A′O⊥OA,A′O⊥OB,
∴A′O⊥平面ABCD,
∴VC-ADD′=VD′-ACD=VA′-ACD=
S△ACD•A′O=
.
∵BC∥A′D′,且BC=A′D′,
∴A′BCD′是平行四边形,
∴A′B∥CD′,
又∵A′B?平面B′CD′,CD′?B′CD′,
∴A′B∥面B′CD′,
又A′B?面A′BD,A′D?面A′BD,且A′B∩A′D=A′,
∴平面A′BD∥平面B′CD′.
(2)解:∵A′O=1,AB=AA′=A′D=
| 2 |
∴A′O2+OA2=AA'2,A′O2+OB2=A′B2,
∴A′O⊥OA,A′O⊥OB,
∴A′O⊥平面ABCD,
∴VC-ADD′=VD′-ACD=VA′-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查平面与平面平行的证明,考查三棱锥C-ADD′的体积VC-ADD′,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
已知函数f(x)是奇函数,且当x>0时,f(x)=x2+
,则f(-1)=( )
| 1 |
| x |
| A、-2 | B、0 | C、1 | D、2 |
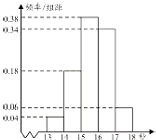 高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图. 如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1.
如图,多面体ABCDEFG中,四边形ABCD,CDEF都是边长为2的正方形,DE⊥平面ABCD,AG⊥平面ABCD,且AG=1.