题目内容
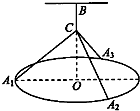如图，一个圆环O直径为4m，通过铁丝CA1，CA2，CA3，BC（A1，A2，A3是圆上三等分点）悬挂在B处，圆环呈水平状态，并距天花板2m，记四段铁丝总长为y（m）．（1）按下列要求建立函数关系：
（ⅰ）设∠CA1O=θ（rad），将y表示为θ的函数，并写出函数定义域；
（ⅱ）设BC=x（m），将y表示为x的函数，并写出函数定义域；
（2）请你选用（1）中的一个函数关系，求铁丝总长y的最小值．（精确到0.1m，取
| 2 |
考点：函数解析式的求解及常用方法
专题：函数的性质及应用,导数的综合应用
分析：（1）（i）由题意，求出CA1、BC的表达式，即得函数y的解析式；
（ii）由BC得出CO，求出CA1，即得函数y的解析式；
（2）由（i）求出y′，利用导数求出y的最小值，即得铁丝总长的最小值．
（ii）由BC得出CO，求出CA1，即得函数y的解析式；
（2）由（i）求出y′，利用导数求出y的最小值，即得铁丝总长的最小值．
解答：
解：（1）（i）由题意，CA1=CA2=CA3，
∵OA1=2，∴CA1=
，OC=2tanθ，BC=2-2tanθ，
∴y=2-2tanθ+3×
=2+
；
∵BC＞0，∴tanθ＜1，∴θ∈（0，
），
∴y=2+
，θ∈（0，
）；
（ii）∵BC=x，∴CO=2-x，CA1=
=
，
∴y=x+3
，x∈（0，2）；
（2）由（i）得，y′=
=
，
令y′=0，得sinθ=
；
∵θ∈（0，
），∴sinθ∈（0，
），∴
∈（0，
）；
设sinθ0=
，θ0∈（0，
），
∵x∈（0，θ0）时，y′＜0，x=θ0时，y′=0，x∈（θ0，
）时，y′＞0；
∴当sinθ=
时，y取得极小值，也是最小值；
此时，cosθ=
=
，
y=4
+2≈7.6（m）；
∴铁丝总长y的最小值为7.6m．
∵OA1=2，∴CA1=
| 2 |
| cosθ |
∴y=2-2tanθ+3×
| 2 |
| cosθ |
| 6-2sinθ |
| cosθ |
∵BC＞0，∴tanθ＜1，∴θ∈（0，
| π |
| 4 |
∴y=2+
| 6-2sinθ |
| cosθ |
| π |
| 4 |
（ii）∵BC=x，∴CO=2-x，CA1=
| 22+(2-x)2 |
| x2-4x+8 |
∴y=x+3
| x2-4x+8 |
（2）由（i）得，y′=
| (-2cosθ)cosθ-(6-2sinθ)(-sinθ) |
| cos2θ |
| 6sinθ-2 |
| cos2θ |
令y′=0，得sinθ=
| 1 |
| 3 |
∵θ∈（0，
| π |
| 4 |
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
设sinθ0=
| 1 |
| 3 |
| π |
| 4 |
∵x∈（0，θ0）时，y′＜0，x=θ0时，y′=0，x∈（θ0，
| π |
| 4 |
∴当sinθ=
| 1 |
| 3 |
此时，cosθ=
| 1-sin2θ |
2
| ||
| 3 |
y=4
| 2 |
∴铁丝总长y的最小值为7.6m．
点评：本题考查了函数的性质与应用问题，解题时应列出函数的解析式，求出函数的定义域，利用导数求函数的最值，是综合题．
练习册系列答案
相关题目
已知a=log0.53，b=0.5-3，c=3-0.5，试比较a，b，c的大小为（ ）
| A、a＜b＜c |
| B、a＜c＜b |
| C、c＜b＜a |
| D、c＜a＜b |
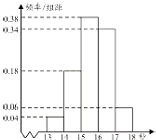高二某班50名学生在一次百米测试中，成绩全部都介于13秒到18秒之间，将测试结果按如下方式分成五组，第一组[13，14），第二组[14，15）…第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
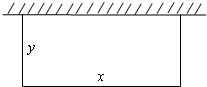一段长为20米的篱笆围成一个一边靠墙的矩形菜园，墙长18米．如图，设菜园与墙平行的边长为x米，另一边长为y米．
如图，多面体ABCDEFG中，四边形ABCD，CDEF都是边长为2的正方形，DE⊥平面ABCD，AG⊥平面ABCD，且AG=1．