题目内容
已知命题P:
≥0,命题Q:|1-
|<1,若P是真命题,Q是假命题,求实数x的取值范围.
| x+1 |
| x-3 |
| x |
| 2 |
考点:复合命题的真假
专题:不等式的解法及应用,简易逻辑
分析:求出命题P、Q为真命题时x的取值范围,再求P是真命题、Q是假命题时x的取值范围.
解答:
解:∵
≥0,
∴
,或
,
解得x≤-1,或x>3;
又∵|1-
|<1,
∴-1<1-
<1
-2<-
<0
∴4>x>0
当P是真命题,Q是假命题时,
,
解得x≤-1,或x≥4;
∴实数x的取值范围是{x|x≤-1,或x≥4}.
| x+1 |
| x-3 |
∴
|
|
解得x≤-1,或x>3;
又∵|1-
| x |
| 2 |
∴-1<1-
| x |
| 2 |
-2<-
| x |
| 2 |
∴4>x>0
当P是真命题,Q是假命题时,
|
解得x≤-1,或x≥4;
∴实数x的取值范围是{x|x≤-1,或x≥4}.
点评:本题考查了复合命题的真假性问题,也考查了不等式的解法与应用问题,解题时应熟记复合命题的真值表,是基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
函数f(x)=
+lg(3x+1)的定义域为( )
| 2x2 | ||
|
A、(-
| ||||
B、(-
| ||||
C、(-
| ||||
D、(-∞,
|
 如图,焦点在x轴的椭圆C:
如图,焦点在x轴的椭圆C: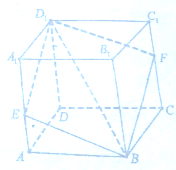 如图,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的平面分别交AA1,CC1于点E,F.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的平面分别交AA1,CC1于点E,F.