题目内容
11．已知x、y满足$\left\{\begin{array}{l}{|x|≤1}\\{|x-y|≤1}\end{array}\right.$，则z=x+y+1的最大值为4．分析 由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求出最优解的坐标，代入目标函数得答案．
解答 解：由约束条件$\left\{\begin{array}{l}{|x|≤1}\\{|x-y|≤1}\end{array}\right.$作出可行域如图，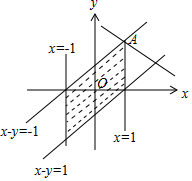
联立$\left\{\begin{array}{l}{x=1}\\{x-y=-1}\end{array}\right.$，解得A（1，2），
化目标函数z=x+y+1为y=-x+z-1，由图可知，当直线y=-x+z-1过A时，直线在y轴上的截距最大，z有最大值为4．
故答案为：4．
点评 本题考查简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．已知曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x，则该曲线的离心率为（ ）
| A． | $\frac{\sqrt{6}}{2}$ | B． | $\sqrt{2}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\sqrt{3}$ |
2．定义在R上的函数y=f（x）在（-∞，a）上是增函数，函数y=f（x+a）是偶函数，当x1＜x2且x1+x2＞2a时，有（ ）
| A． | f（2a-x1）＜f（2a-x2） | B． | f（2a-x1）＞f（2a-x2） | C． | f（2a-x1）=f（2a-x2） | D． | 以上都不正确 |
19．“2x＞1”是“x＞1”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分又不必要条件 |
6．随着教育制度和高考考试制度的改革，高校选拔人才的方式越来越多．某高校向一基地 学校投放了一个保送生名额，先由该基地学校初选出10名优秀学生，然后参与高校设置的 考核，考核设置了难度不同的甲、乙两个方案，每个方案都有M（文化）、N（面试）两个考核内 容，最终选择考核成绩总分第一名的同学定为该高校在基地校的保送生．假设每位同学完成 每个方案中的M、N两个考核内容的得分是相互独立的．根据考核前的估计，某同学完成甲 方案和乙方案的M、N两个考核内容的情况如表：
表1：甲方案
表2：乙方案
已知该同学最后一个参与考核，之前的9位同学的最高得分为125分．
（I）若该同学希望获得保送资格，应该选择哪个方案？请说明理由，并求其在该方案下 获得保送资格的概率；
（II）若该同学选用乙方案，求其所得成绩X的分布列及其数学期望EX．
表1：甲方案
| 考核内容 | M（文化） | N（面试） | ||
| 得分 | 100 | 80 | 50 | 20 |
| 概率 | $\frac{3}{4}$ | $\frac{1}{4}$ | $\frac{3}{4}$ | $\frac{1}{4}$ |
| 考核内容 | M（文化） | N（面试） | ||
| 得分 | 90 | 60 | 30 | 10 |
| 概率 | $\frac{9}{10}$ | $\frac{1}{10}$ | $\frac{9}{10}$ | $\frac{1}{10}$ |
（I）若该同学希望获得保送资格，应该选择哪个方案？请说明理由，并求其在该方案下 获得保送资格的概率；
（II）若该同学选用乙方案，求其所得成绩X的分布列及其数学期望EX．
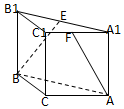如图，ABC-A1B1C1是直三棱柱，∠BCA=90°，点E、F分别是A1B1、A1C1的中点，若BC=CA=AA1，则BE与AF所成角的余弦值为$\frac{\sqrt{30}}{10}$．