题目内容
 四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=1,BC=2,PA⊥底面ABCD.
四棱锥P-ABCD中,底面ABCD是矩形,PA=AB=1,BC=2,PA⊥底面ABCD.(1)求证:平面PDC⊥平面PAD;
(2)在边BC上是否存在一点G,使得PD与平面PAG所成的正弦是
| ||
| 5 |
考点:直线与平面所成的角,平面与平面垂直的判定
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)运用线面垂直的判定和性质,面面垂直的判定定理,即可得证;
(2)在边BC上假设存在一点G,使得PD与平面PAG所成的正弦是
.过D作DO⊥平面PAG,垂足为O,连接PO,
则∠DPO为PD与平面PAG所成的角.运用等积法,得VP-ADG=VD-PAG,即
PA•S△ADG=
DO•S△PAG,即可判断.
(2)在边BC上假设存在一点G,使得PD与平面PAG所成的正弦是
| ||
| 5 |
则∠DPO为PD与平面PAG所成的角.运用等积法,得VP-ADG=VD-PAG,即
| 1 |
| 3 |
| 1 |
| 3 |
解答:
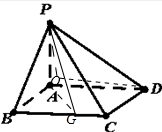 (1)证明:∵PA⊥底面ABCD,
(1)证明:∵PA⊥底面ABCD,
∴PA⊥CD,
∵底面ABCD是矩形,∴CD⊥AD,
∴CD⊥平面PAD,
∵CD?平面PDC,∴平面PDC⊥平面PAD;
(2)在边BC上假设存在一点G,使得PD与平面PAG所成的正弦是
.
过D作DO⊥平面PAG,垂足为O,连接PO,
则∠DPO为PD与平面PAG所成的角.
设BG=x,则△ADG的面积为1,AG=
,
直角三角形PAG的面积为
,
在直角三角形PAD中,PD=
,
由sin∠DPO=
,得DO=PDsin∠DPO=1.
由等积法,得VP-ADG=VD-PAG,即
PA•S△ADG=
DO•S△PAG,
1=
,解得x=
.
故在边BC上一点G,使得BG=
,PD与平面PAG所成的正弦是
.
 (1)证明:∵PA⊥底面ABCD,
(1)证明:∵PA⊥底面ABCD,∴PA⊥CD,
∵底面ABCD是矩形,∴CD⊥AD,
∴CD⊥平面PAD,
∵CD?平面PDC,∴平面PDC⊥平面PAD;
(2)在边BC上假设存在一点G,使得PD与平面PAG所成的正弦是
| ||
| 5 |
过D作DO⊥平面PAG,垂足为O,连接PO,
则∠DPO为PD与平面PAG所成的角.
设BG=x,则△ADG的面积为1,AG=
| 1+x2 |
直角三角形PAG的面积为
| 1 |
| 2 |
| 1+x2 |
在直角三角形PAD中,PD=
| 5 |
由sin∠DPO=
| ||
| 5 |
由等积法,得VP-ADG=VD-PAG,即
| 1 |
| 3 |
| 1 |
| 3 |
1=
| 1 |
| 2 |
| 1+x2 |
| 3 |
故在边BC上一点G,使得BG=
| 3 |
| ||
| 5 |
点评:本题考查直线与平面垂直的判定和性质,面面垂直的判定定理,考查直线与平面所成的角的求法,考查等积法,属于中档题.

练习册系列答案
相关题目