题目内容
设集合A=B={1,2,3,4,5,6},分别从集合A和B中随机各取一个数x,y,确定平面上的一个点P(x,y),记“点P(x,y)满足条件x2+y2≤16”为事件C,则C的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:求出从集合A和B中随机各取一个数x,y的基本事件总数,和满足点P(x,y)满足条件x2+y2≤16的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:∵集合A=B={1,2,3,4,5,6},
分别从集合A和B中随机各取一个数x,y,确定平面上的一个点P(x,y),
共有6×6=36种不同情况,
其中P(x,y)满足条件x2+y2≤16的有:
(1,1),(1,2),(1,3),(2,1),
(2,2),(2,3),(3,1),(3,2),共8个,
∴C的概率P(C)=
=
,
故选:A
分别从集合A和B中随机各取一个数x,y,确定平面上的一个点P(x,y),
共有6×6=36种不同情况,
其中P(x,y)满足条件x2+y2≤16的有:
(1,1),(1,2),(1,3),(2,1),
(2,2),(2,3),(3,1),(3,2),共8个,
∴C的概率P(C)=
| 8 |
| 36 |
| 2 |
| 9 |
故选:A
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
某人计划年初向银行贷款m万元用于买房.他选择10年期贷款,偿还贷款的方式为:分10次等额归还,每年一次,并从借后次年年初开始归还,若10年期贷款的年利率为r,且每年利息均按复利计算(即本年的利息计入次年的本金生息),则每年应还款金额为( )元.
A、
| ||
B、
| ||
C、
| ||
D、
|
当x∈[1,2]时,函数f(x)=ax2+4(a+1)x-3在x=2时取得最大值,则实数a的取值范围是( )
A、[-
| ||
| B、[0,+∞) | ||
| C、[1,+∞) | ||
D、[
|
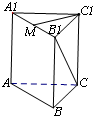 如图,在直三棱柱ABC-A1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,AA1=2,点M是A1B1的中点,则异面直线C1M与B1C所成角的余弦值为( )
如图,在直三棱柱ABC-A1B1C1的底面ABC中,CA=CB=1,∠BCA=90°,AA1=2,点M是A1B1的中点,则异面直线C1M与B1C所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,角A,B,C所对应的边分别为a,b,c,若A=60°,b=1,且△ABC的面积为
,则边a的值为( )
| 3 |
A、2
| ||
B、
| ||
C、
| ||
| D、3 |
对于数25,规定第1次操作为23+53=133,第2次操作为13+33+33=55,如此反复操作,则第100次操作后得到的数是( )
| A、25 | B、250 |
| C、55 | D、133 |
函数f(x)=x•ex,则f′(1)=( )
| A、2e | B、1+e | C、1 | D、2 |
在△ABC中,已知a=
,b=
,B=45°,则角A为( )
| 3 |
| 2 |
| A、60° |
| B、150° |
| C、60°或 150° |
| D、60°或120° |
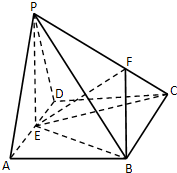 如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE=
如图,四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,AB=2,PE=