题目内容
袋内装有6个球,每个球上都记有从1到6的一个号码,设号码为n的重n2-6n+12克,这些求等可能地从袋里取出(不受重量、号码的影响)
(1)如果任意取出1球,求其重量大于号码数的概率;
(2)如果不放回地任意取出2球,求它们重量相等的概率.
(1)如果任意取出1球,求其重量大于号码数的概率;
(2)如果不放回地任意取出2球,求它们重量相等的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:(1)任意取出1球,共有6种等可能的方法,要求其重量大于号码数的概率,我们只要根据号码为n的球的重量为n2-6n+12克,构造关于n的不等式,解不等式即可得到满足条件的基本事件的个数,代入古典概型公式即可求解.
(2)我们要先计算出不放回地任意取出2球的基本事件总个数,然后根据重量相等构造方程解方程求出满足条件的基本事件的个数,代入古典概型计算公式即可求解.
(2)我们要先计算出不放回地任意取出2球的基本事件总个数,然后根据重量相等构造方程解方程求出满足条件的基本事件的个数,代入古典概型计算公式即可求解.
解答:
解:(1)由题意,任意取出1球,共有6种等可能的方法.
由不等式n2-6n+12>n,得n>4或n<3.
所以n=1,2或n=5,6,
于是所求概率为P=
=
.
(2)如果不放回的任意取出2个球,这两个球的编号可能的情况为:1、2; 1、3; 1、4;1、5;1、6;
2、3; 2、4; 2、5; 2、6; 3、4; 3、5; 3、6; 4、5; 4、6; 5、6,共15种情况.
设编号为m的球与编号为n的球重量相等,则有m2-6n+12=n2-6n+12,即 (m-n)(m+n-6)=0,
结合题意可得m+n-6=0,即m+n=6.
故满足m+n=6的情况为1、5; 2、4,共两种情形.
故所求事件的概率为
.
由不等式n2-6n+12>n,得n>4或n<3.
所以n=1,2或n=5,6,
于是所求概率为P=
| 4 |
| 6 |
| 2 |
| 3 |
(2)如果不放回的任意取出2个球,这两个球的编号可能的情况为:1、2; 1、3; 1、4;1、5;1、6;
2、3; 2、4; 2、5; 2、6; 3、4; 3、5; 3、6; 4、5; 4、6; 5、6,共15种情况.
设编号为m的球与编号为n的球重量相等,则有m2-6n+12=n2-6n+12,即 (m-n)(m+n-6)=0,
结合题意可得m+n-6=0,即m+n=6.
故满足m+n=6的情况为1、5; 2、4,共两种情形.
故所求事件的概率为
| 2 |
| 15 |
点评:本题主要考查排列、组合及简单计数问题,古典概型,属于中档题.

练习册系列答案
相关题目
设x∈(0,
),则“xsinx<1”是“xsin2x<1”的( )
| π |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
 如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=
如图所示的韦恩图中A,B是非空集合,定义集合A*B为阴影部分表示的集合,若x,y∈R,A={x|y=| 2x-x2 |
| A、{x|0<x<2} |
| B、{x|1<x<2} |
| C、{x|0≤x≤1或x≥2} |
| D、{x|0≤x≤1或x>2} |
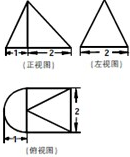
一个几何体的三视图如图,其俯视图是一个等边三角形,则这个几何体的体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、(4+π)
|
方程lgx+x=0在下列的哪个区间内有实数解( )
A、[-10,-
| ||
| B、(-∞,0] | ||
| C、[1,10] | ||
D、[
|
 如图所示,四棱锥P-ABCD的底面ABCD为直角梯形,且AD∥BC,AD⊥AB,E是PC的中点,PA=BC=2AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图所示,四棱锥P-ABCD的底面ABCD为直角梯形,且AD∥BC,AD⊥AB,E是PC的中点,PA=BC=2AD=1,AB=2,∠PAB=120°,∠PBC=90°.