题目内容
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为4π,且其图象向右平移$\frac{π}{5}$个单位后得到函数g(x)=sinωx的图象,则φ等于( )| A. | -$\frac{π}{10}$ | B. | -$\frac{π}{5}$ | C. | $\frac{π}{10}$ | D. | $\frac{π}{5}$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:∵函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为4π,∴$\frac{2π}{ω}$=4π,∴ω=$\frac{1}{2}$,f(x)=sin($\frac{1}{2}$x+φ).
把它的图象向右平移$\frac{π}{5}$个单位后得到函数g(x)=sin[$\frac{1}{2}$(x-$\frac{π}{5}$)+φ]=sin$\frac{1}{2}$x 的图象,
∴-$\frac{π}{10}$+φ=2kπ,k∈Z,故可取φ=$\frac{π}{10}$,
故选:C.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为30°,且|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=2,则$|{2\vec a-\vec b}|$等于( )
| A. | 4 | B. | 2 | C. | 13 | D. | $2\sqrt{7}$ |
9.将函数f(x)=2sin(πx)的图象向左平移φ(0<φ<4)个单位,得到函数y=g(x)的图象,若实数x1,x2满足|f(x1)-g(x2)|=4,且|x1-x2|min=2,则φ=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
14.如果命题“p∧q”是假命题,“¬p”是真命题,那么( )
| A. | 命题p一定是真命题 | |
| B. | 命题q一定是真命题 | |
| C. | 命题q一定是假命题 | |
| D. | 命题q可以是真命题也可以是假命题 |
15.在技术工程中,常用到双曲正弦函数$shx=\frac{{{e^x}-{e^{-x}}}}{2}$和双曲余弦函数$chx=\frac{{{e^x}-{e^{-x}}}}{2}$,其实双曲正弦函数和双曲线余弦函数与我们学过的正弦和余弦函数相似,比如关于正、余弦函数有cos(x+y)=cosxcosy-sinxsiny成立,而关于双曲正、余弦函数满足ch(x+y)=chxchy-shxshy,请你类比关系式,得出关于双曲正弦、双曲余弦函数的关系中不正确的是( )
| A. | sh(x+y)=shxchy+chxshy | B. | sh2x=2shxchx | ||
| C. | ch2x=2sh2x-1 | D. | ch2x+sh2x=1 |
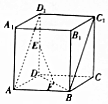 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是边长2的正方形,E,F分别为线段DD1,BD的中点.