题目内容
15.在技术工程中,常用到双曲正弦函数$shx=\frac{{{e^x}-{e^{-x}}}}{2}$和双曲余弦函数$chx=\frac{{{e^x}-{e^{-x}}}}{2}$,其实双曲正弦函数和双曲线余弦函数与我们学过的正弦和余弦函数相似,比如关于正、余弦函数有cos(x+y)=cosxcosy-sinxsiny成立,而关于双曲正、余弦函数满足ch(x+y)=chxchy-shxshy,请你类比关系式,得出关于双曲正弦、双曲余弦函数的关系中不正确的是( )| A. | sh(x+y)=shxchy+chxshy | B. | sh2x=2shxchx | ||
| C. | ch2x=2sh2x-1 | D. | ch2x+sh2x=1 |
分析 由余弦的二倍角公式可知,ch2x=1-2sh2x,可得结论.
解答 解:类比关系式,得sh(x+y)=shxchy+chxshy,sh2x=2shxchx,ch2x+sh2x=1正确.
由余弦的二倍角公式可知,ch2x=1-2sh2x,即C不正确;
故选C.
点评 本题考查类比推理,考查学生的探究能力,属于基础题型.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
4.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为4π,且其图象向右平移$\frac{π}{5}$个单位后得到函数g(x)=sinωx的图象,则φ等于( )
| A. | -$\frac{π}{10}$ | B. | -$\frac{π}{5}$ | C. | $\frac{π}{10}$ | D. | $\frac{π}{5}$ |
6.将石子摆成如图的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第2 016项与5的差,即a2016-5=( )


| A. | 2 018×2 014 | B. | 2 018×2 013 | C. | 1 011×2 015 | D. | 1 010×2 012 |
3.y=5-sin2x-4cosx最小值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | -1 |
10.已知α是△ABC的一个内角,且$sinα+cosα=\frac{1}{5}$,
(Ⅰ)判断△ABC的形状;
(Ⅱ)求$\frac{{sinxcosx+{{sin}^2}x}}{1-tanx}$的值.
(Ⅰ)判断△ABC的形状;
(Ⅱ)求$\frac{{sinxcosx+{{sin}^2}x}}{1-tanx}$的值.
20.已知f(x)=2xf′(1)+lnx,则f′(1)=( )
| A. | -e | B. | -1 | C. | 1 | D. | e |
7.如图所示,两个阴影部分的面积之和可表示为( )
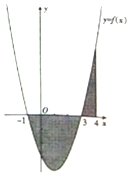

| A. | $\int_{-1}^4{f(x)}dx$ | B. | $-\int_{-1}^4{f(x)}dx$ | ||
| C. | $\int_3^4{f(x)}dx-\int_{-1}^3{f(x)dx}$ | D. | $\int_{-1}^3{f(x)}dx-\int_3^4{f(x)dx}$ |
5.某地区的年降水量在下列范围内的概率如表所示:
则年降水量在[200,300](mm)范围内的概率为0.51,年降水量在[300,400](mm)范围内的概率为0.22.
| 年降水量(mm) | [200,250] | [250,300] | [300,350] | [350,400] |
| 概率 | 0.30 | 0.21 | 0.14 | 0.08 |