题目内容
11.执行如图所示的程序框图,若输入的x,y∈R,则输出t的最大值为( )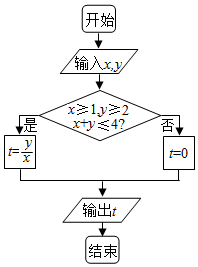
| A. | 1 | B. | 3 | C. | 2 | D. | 0 |
分析 分析框图可知,本题是求可行域$\left\{\begin{array}{l}{\stackrel{x≥1}{y≥2}}\\{x+y≤4}\end{array}\right.$内,目标函数t=$\frac{y}{x}$最大值,画出可行域,求得取得最大值的点的坐标,得出最大值即可.
解答 解:由程序框图知:本题是求可行域$\left\{\begin{array}{l}{\stackrel{x≥1}{y≥2}}\\{x+y≤4}\end{array}\right.$内,t=$\frac{y}{x}$的最大值,
画出可行域如图: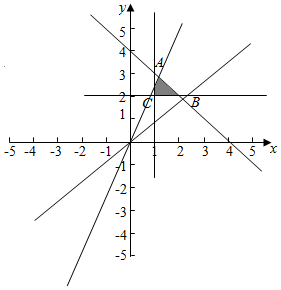
由于t=$\frac{y}{x}$为经过可行域的一点与原点的直线的斜率,可得当直线经过OA时斜率最大,
由$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$,解得,A(1,3),此时,t=$\frac{y}{x}$=$\frac{3}{1}$=3.
故选:B.
点评 本题借助选择结构的程序框图考查了线性规划问题的解法,根据框图的流程判断算法的功能是解题的关键,属于基础题.

练习册系列答案
相关题目
16.已知a,b∈R,且a-1+(b+2)i=0.i为虚数单位,则复数(a+bi)2在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.某高中为了解全校学生每周参加体育运动的情况,随机从全校学生中抽取100名学生,统计他们每周参与体育运动的时间如下:
(1)作出样本的频率分布直方图;
(2)①估计该校学生每周参与体育运动的时间的中位数及平均数;
②若该校有学生3000人,根据以上抽样调查数据,估计该校学生每周参与体育运动的时间不低于8小时的人数.
| 每周参与运动的时间(单位:小时) | [0,4) | [4,8) | [8,12) | [12,16) | [16,20] |
| 频数 | 24 | 40 | 28 | 6 | 2 |
(2)①估计该校学生每周参与体育运动的时间的中位数及平均数;
②若该校有学生3000人,根据以上抽样调查数据,估计该校学生每周参与体育运动的时间不低于8小时的人数.
 如图,在平行四边形ABCD中,已知$\overrightarrow{|AB|}$=8,$\overrightarrow{|AD|}$=5,$\overrightarrow{CP}=3\overrightarrow{PD}$,$\overrightarrow{AP}•\overrightarrow{BP}=2$,则$\overrightarrow{AB}•\overrightarrow{AD}$=22.
如图,在平行四边形ABCD中,已知$\overrightarrow{|AB|}$=8,$\overrightarrow{|AD|}$=5,$\overrightarrow{CP}=3\overrightarrow{PD}$,$\overrightarrow{AP}•\overrightarrow{BP}=2$,则$\overrightarrow{AB}•\overrightarrow{AD}$=22.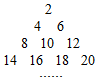 将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.
将正偶数排列如图,其中第i行和第j列的数表示为aij=(i,j∈N+),例如a43=18,若aij=2016,则i+j=63.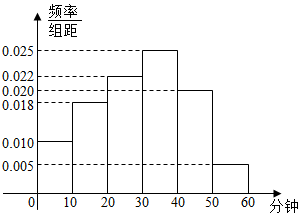 某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.