题目内容
18.已知函数f(x)=cos2x-2sinxcosx-sin2x.(1)求f(x)的最小正周期;
(2)当x∈[0,$\frac{π}{2}$]时,求f(x)的最小值及取得最小值时x的值.
分析 (1)将函数进行化简,结合三角函数的图象和性质即可求函数y=f(x)图象的最小正周期;
(2)根据x∈[0,$\frac{π}{2}$],求出f(x)的范围,结合三角函数的图象和性质即可求f(x)的最小值及取得最小值时x的值.
解答 解:f(x)=cos2x-2sinxcosx-sin2x=cos2x-sin2x=$\sqrt{2}cos(2x+\frac{π}{4})$
(1)最小正周期$T=\frac{2π}{ω}$=$\frac{2π}{2}=π$
(2)∵x∈[0,$\frac{π}{2}$]即$0≤x≤\frac{π}{2}$,∴$\frac{π}{4}≤2x+\frac{π}{4}≤\frac{5π}{4}$;
结合三角函数的图象和性质:$2x+\frac{π}{4}=\frac{5π}{4}$时,$f(x)min=\sqrt{2}cos\frac{5π}{4}=-1$
由:$2x+\frac{π}{4}=\frac{5π}{4}$,解得x=$\frac{π}{2}$.
∴当x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-1,取得最小值时x的值为$\frac{π}{2}$.
故:f(x)的最小正周期为π;x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-1,取得最小值时x的值为$\frac{π}{2}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
相关题目
13.如表是某小卖部一周卖出热茶的杯数与当天气温的对比表:
若热茶杯数y与气温x近似地满足线性关系,则其关系式最接近的是( )
| 气温/℃ | 18 | 13 | 10 | 4 | 0 |
| 杯数 | 24 | 34 | 39 | 51 | 62 |
| A. | y=x+6 | B. | y=-x+42 | C. | y=-2x+60 | D. | y=-3x+78 |
7.已知双曲线kx2-2ky2=4的一条准线是y=1,则实数k的值是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | 1 | D. | -1 |
8.若f'(x0)=2,则$\lim_{△x→0}\frac{{f({x_0})-f({x_0}+△x)}}{△x}$=( )
| A. | -1 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
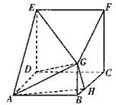 在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.
在多面体ABCDEFG中,四边形ABCD与CDEF均为边长为4的正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH.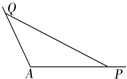 如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.
如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.