题目内容
9.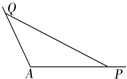 如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.
如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.(1)若AP=5,PQ=3$\sqrt{5}$,求AQ的长;
(2)设∠APQ=α,∠AQP=β,且cosα=$\frac{12}{13}$,求cos(α+β)和cos(2α+β)的值.
分析 (1)由A为钝角,根据同角三角函数的基本关系,求得cosA,利用余弦定理,AQ2+8AQ-20=0,求得AQ的值;
(2)由三角形的内角和定理求得sin(α+β)=sin(π-A)=sinA=$\frac{3}{5}$,即可求得cos(α+β),cos(2α+β)=cos[(α+β)+α],根据两角和的余弦公式即可求得cos(2α+β)的值.
解答 解:(1)角A为钝角,sinA=$\frac{3}{5}$,
∴cosA<0,cosA=-$\sqrt{1-si{n}^{2}A}$=-$\frac{4}{5}$,…(1分)
在△APQ中,由余弦定理得:PQ2=AP2+AQ2-2AP•AQcosA,…(2分)
∴AQ2+8AQ-20=0,…(4分)
解:AQ=2或AQ=-10(舍去负值),
∴AQ=2; …(5分)
(2)由cosα=$\frac{12}{13}$,sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{5}{13}$,
在三角形APQ中,A+α+β=π,
∵sin(α+β)=sin(π-A)=sinA=$\frac{3}{5}$,
cos(α+β)=-cosA=$\frac{4}{5}$,…(6分)
∴cos(2α+β)=cos[(α+β)+α]=cos(α+β)cosα-sin(α+β)sinα,
=$\frac{4}{5}$•$\frac{12}{13}$-$\frac{3}{5}$•$\frac{5}{13}$,
=$\frac{33}{65}$. …(8分)
∴cos(2α+β)=$\frac{33}{65}$. …(10分)
点评 本题考查余弦定理的应用,考查两角和差的正余弦公式,同角三角函数的基本关系,三角形内角和定理,考查计算能力,属于中档题.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案| A. | [1,$\frac{3}{2}$) | B. | [1,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2) | D. | [$\frac{3}{2}$,2] |
| A. | 10 | B. | 30 | C. | 45 | D. | 120 |
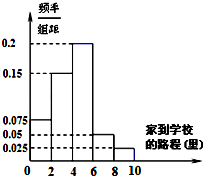 某高中地处市区,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
某高中地处市区,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:①若把家到学校的距离分为五个区间:[0,2)、[2,4)、[4,6)、[6,8)、[8,10),午休的走读生的分布情况如频率分布直方图所示;
②走读生是否午休与下午开始上课的时间有着密切的关系. 5次调查结果的统计表如表:
| 下午开始 上课时间 | 2:10 | 2:20 | 2:30 | 2:40 | 2:50 |
| 平均每天 午休人数 | 250 | 350 | 500 | 650 | 750 |
(2)如果把下午开始上课时间2:10作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试列出x与y的统计表,并根据表中的数据求平均每天午休人数$\widehat{y}$与上课时间x之间的线性回归方程$\widehat{y}$=bx+a;
(3)预测当下午上课时间推迟到3:00时,家距学校的路程在6里路以上的走读生中约有多少人午休?
(注:线性回归直线方程系数公式b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.)