关于x的不等式a•2x+4x+1＞0恒成立.求常数a的取值范围．题目和参考答案——青夏教育精英家教网——

题目内容

关于x的不等式a•2^x+4^x+1＞0恒成立，求常数a的取值范围

．

考点：指数型复合函数的性质及应用

专题：函数的性质及应用

分析：将不等式恒成立转化为参数恒成立，利用基本不等式的性质即可得到结论．

解答： 解：由a•2^x+4^x+1＞0得a•2^x＞-4^x-1，
∴a＞

-4x-1

2x

=-(2x+

1

2x

)，
∵2x+

1

2x

≥2

2x?

1

2x

=2，
∴-(2x+

1

2x

)≤-2，
即a＞-2，
故答案为：（-2，+∞）．

点评：本题主要考查不等式恒成立问题，将不等式进行转化利用基本不等式进行求解是解决本题的关键．

练习册系列答案

高中新课程暑假作业济南出版社系列答案

Happy欢乐假期作业济南出版社系列答案

本土教辅赢在暑假高效假期总复习云南科技出版社系列答案

暑假作业北京艺术与科学电子出版社系列答案

黄冈状元成才路暑假作业新疆人民出版社系列答案

暑假特训浙江大学出版社系列答案

名师一号假期作业暑假作业河北教育出版社系列答案

第三学期赢在暑假系列答案

暑假作业宁夏人民教育出版社系列答案

优化学习暑假40天江苏人民出版社系列答案

相关题目

某市共有100万居民的月收入是通过“工资薪金所得”得到的，如图是抽样调查后得到的工资薪金所得X的频率分布直方图．工资薪金个人所得税税率表如表所示．表中“全月应纳税所得额”是指“工资薪金所得”减去3500元所超出的部分（3500元为个税起征点，不到3500元不缴税）．工资个税的计算公式为：“应纳税额”=“全月应纳税所得额”乘以“适用税率”减去“速算扣除数”．

全月应纳税所得额	适用税率（%）	速算扣除数
不超过1500元	3	0
超过1500元至4500元	10	105
超过4500元至9000元	20	555
…	…	…

例如：某人某月“工资薪金所得”为5500元，则“全月应纳税所得额”为5500-3500=2000元，应纳税额为2000×10%-105=95（元）
在直方图的工资薪金所得分组中，以各组的区间中点值代表该组的各个值，工资薪金所得落入该区间的频率作为x取该区间中点值的概率．
（Ⅰ）试估计该市居民每月在工资薪金个人所得税上缴纳的总税款；
（Ⅱ）设该市居民每月从工资薪金所得交完税后，剩余的为其月可支配额y（元），试求该市居民月可支配额y的数学期望．

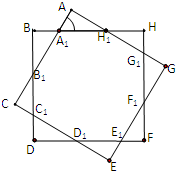如图，制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形．由对称性，图中8个三角形都是全等的三角形，设∠AA₁H₁=α．
（1）试用α表示△AA₁H₁的面积；
（2）求八角形所覆盖面积的最大值，并指出此时α的大小．

=(12，-t)为直线3x-4y+21=0的方向向量，则t=

已知△ABC的顶点A（4，0），B（0，2），C（m+4，2m+2），若△ABC为钝角三角形，则m的取值范围是

已知A（1，-1），B（2，1），C（t，5）三点在同一直线上，则t=

若sin（α-3π）=2cos（α-4π），则

sin(α-π)+5cos(5π-α)

π-α)-sin(-α)

过两点A（4，y），B（2，-3）的直线的倾斜角是135°，则y=（　　）